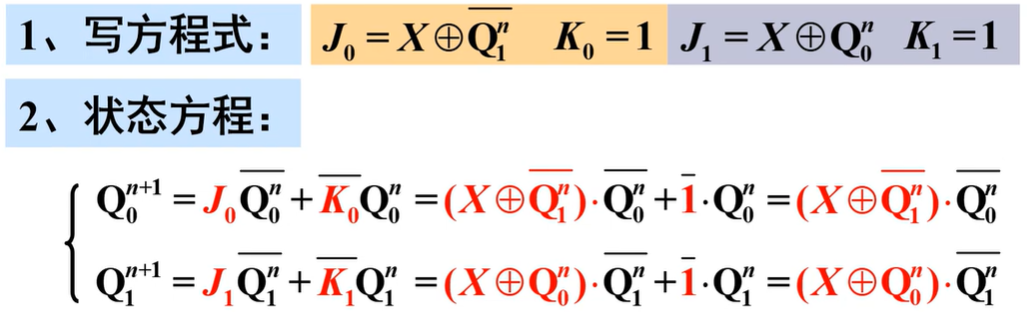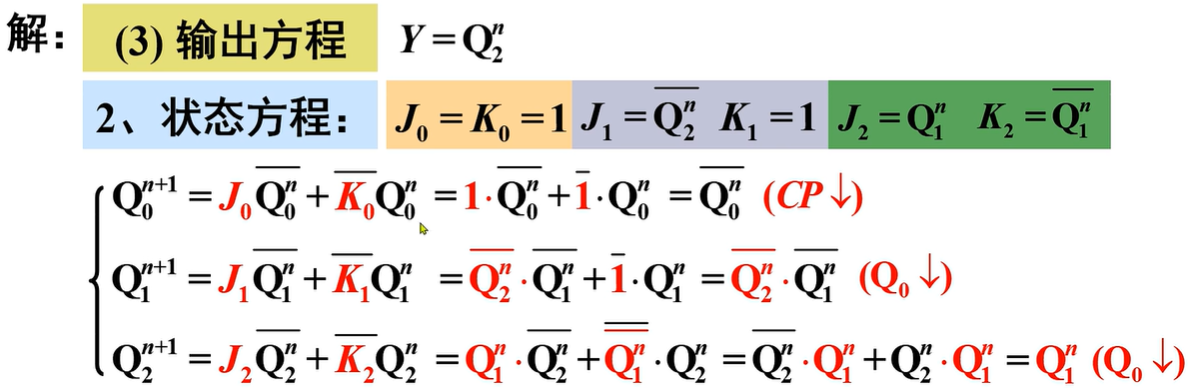时序逻辑电路_分析和设计¶
约 2082 个字 66 张图片 预计阅读时间 10 分钟
内容总览
- 时序逻辑电路的分析和设计
概述¶
时序逻辑电路的基本特性¶
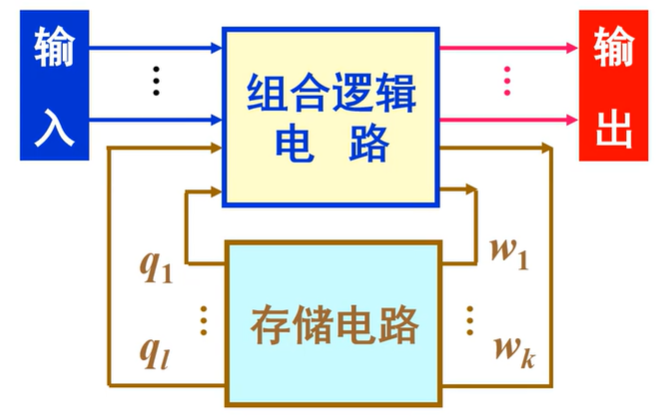
时序逻辑电路(Sequential Logic Circuit),简称为时序电路
定义:任何时刻电路的输出,不仅和该时刻的输入信号有关,而且还取决于电路原来的状态
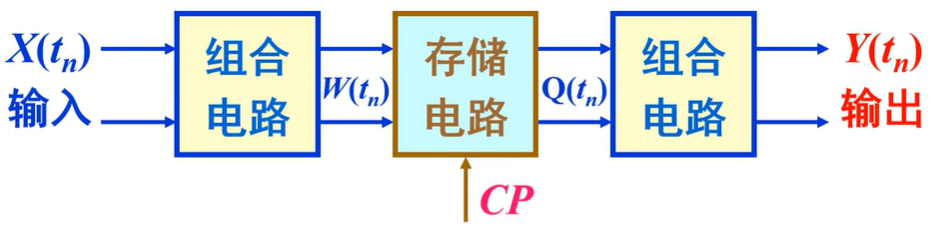
特点:由存储电路和组合逻辑电路组成,与时间因素(CP)有关
时序逻辑电路的类型¶
按逻辑功能分¶
- 计数器
- 寄存器
- 移位寄存器
- 读/写存储器(RAM)
- 顺序脉冲发生器
按电路结构分¶
- 同步时序逻辑电路
- 所有触发器的时钟端连在一起,所有触发器在同一个时钟脉冲CP控制下同步工作
- 异步时序逻辑电路
- 时钟脉冲CP只触发部分触发器,其余触发器由电路内部信号触发。因此,触发器不在同一时钟下同步工作
按信号输出特性分¶
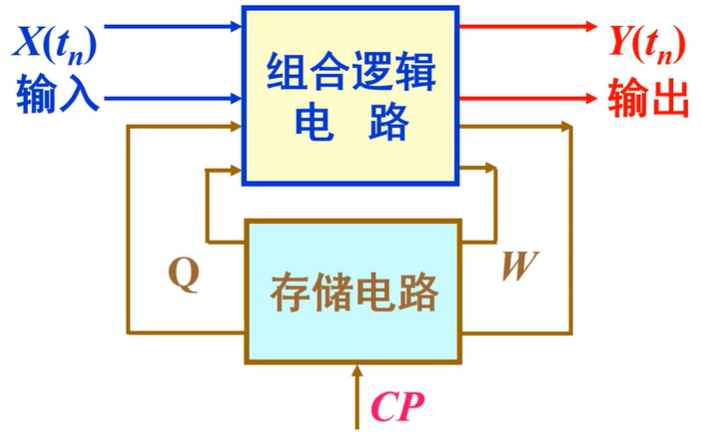
- Mealy型时序逻辑电路
其输入不仅与现态有关,而且还取决于电路的输入,输出方程为\(Y(t_n)=F[X(t_n),Q(t_n)]\)
- Moore型时序逻辑电路
其输出仅取决于电路的现态,输出方程为\(Y(t_n)=F[Q(t_n)]\)
Moore型电路的分析和设计相对于Mealy型会简单很多
时序电路的分析¶
同步时序电路的分析方法¶
基本步骤¶
写方程式:
- 时钟方程:各个触发器时钟信号的逻辑表达式,同步时序电路可省去不写
- 输出方程:时序电路的输出逻辑表达式,通常为现态和输入变量的函数
- 驱动方程:各触发器输入端的逻辑表达式
求状态方程:
- 状态方程:将驱动方程代入相应触发器的特性方程所得到的方程
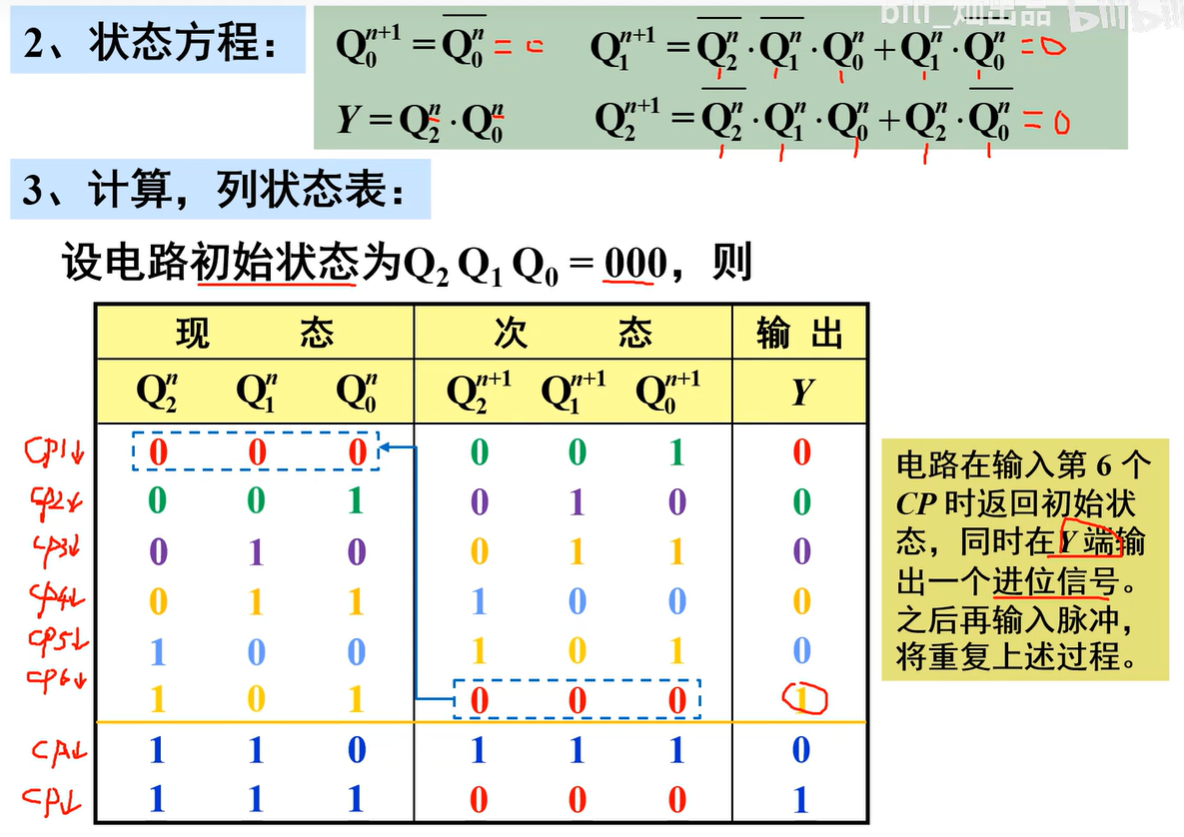
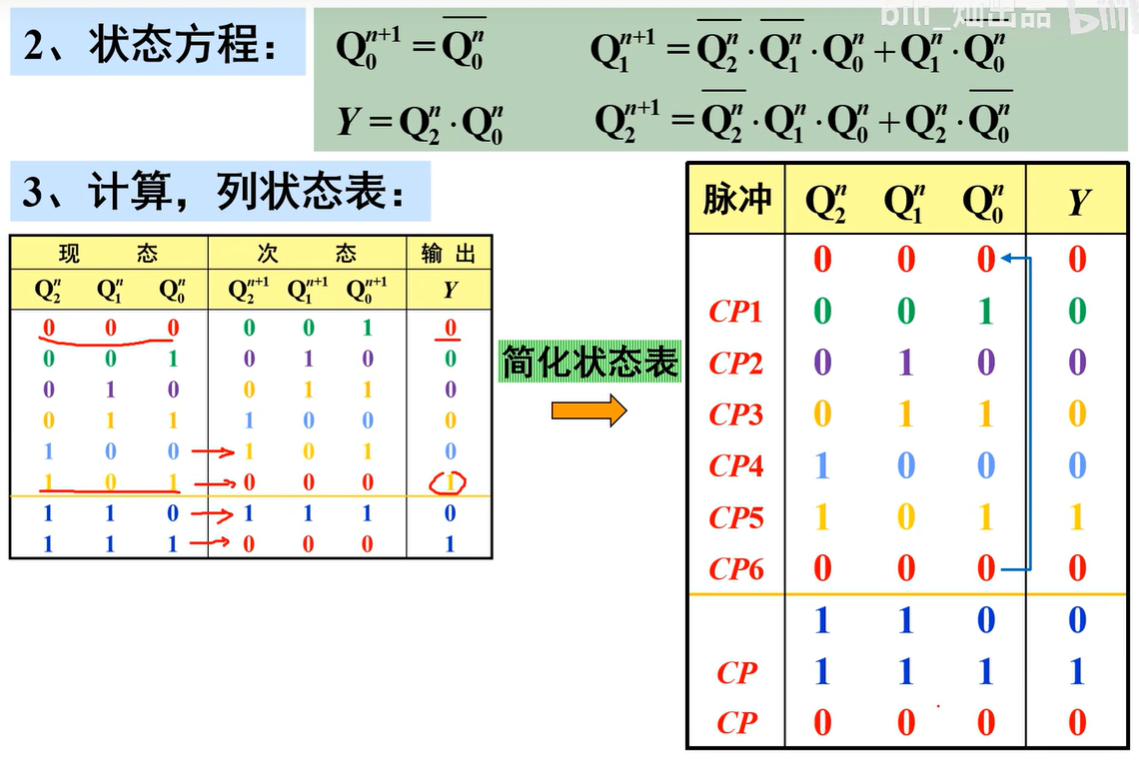
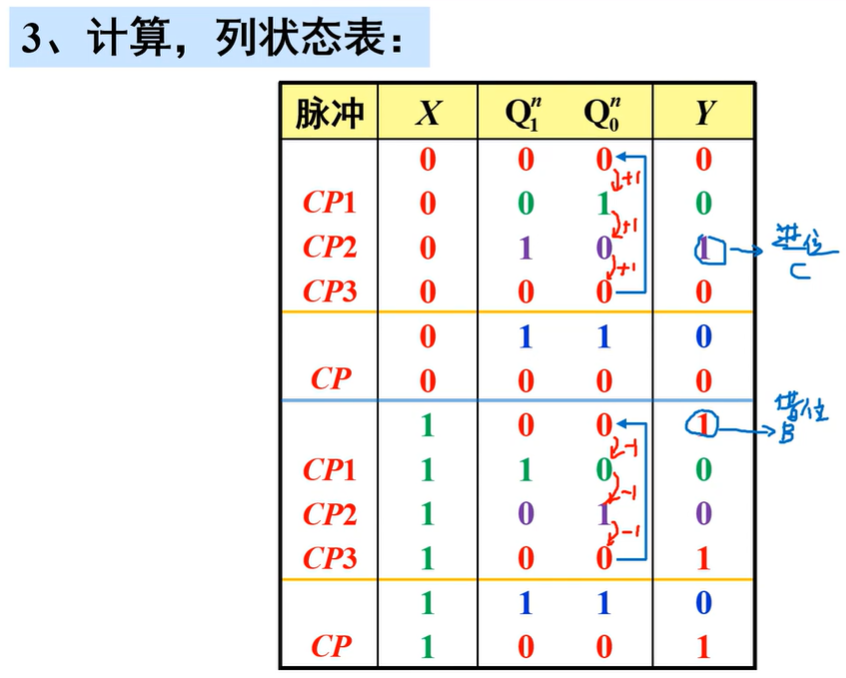
计算、列状态表:
- 状态表:将电路输入和现态的各种取值组合,代入状态方程和输出方程进行计算,求出相应的次态和输出
如现态的起始值已给定,则从给定值开始计算。如没有给定,则可设定一个现态起始值依次进行计算
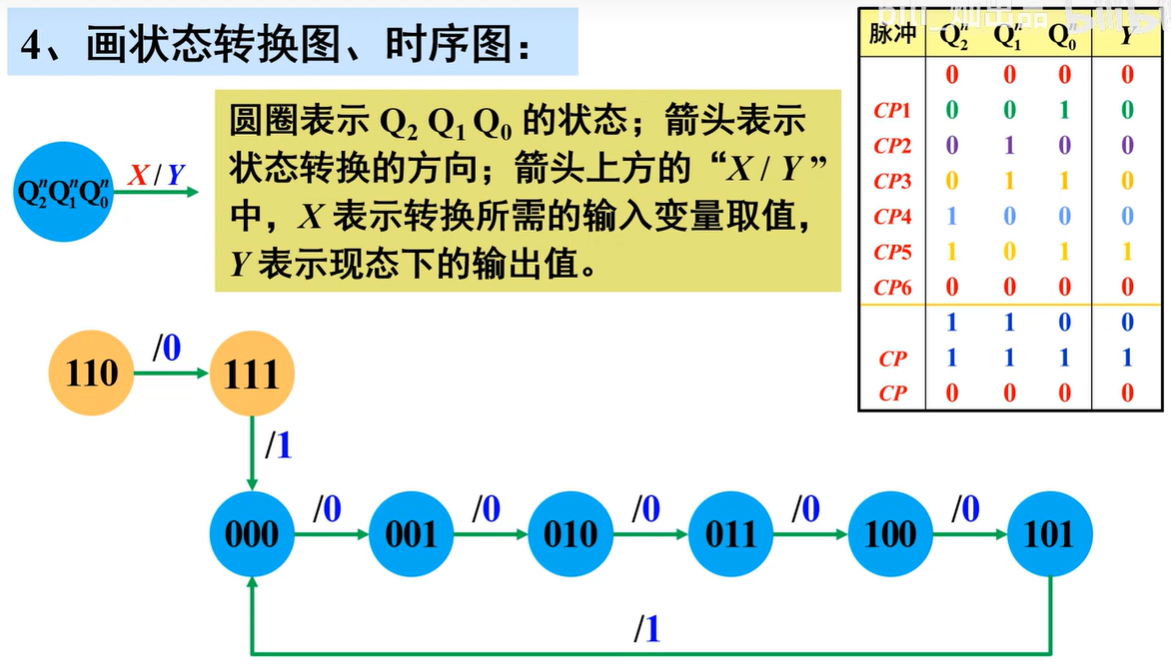
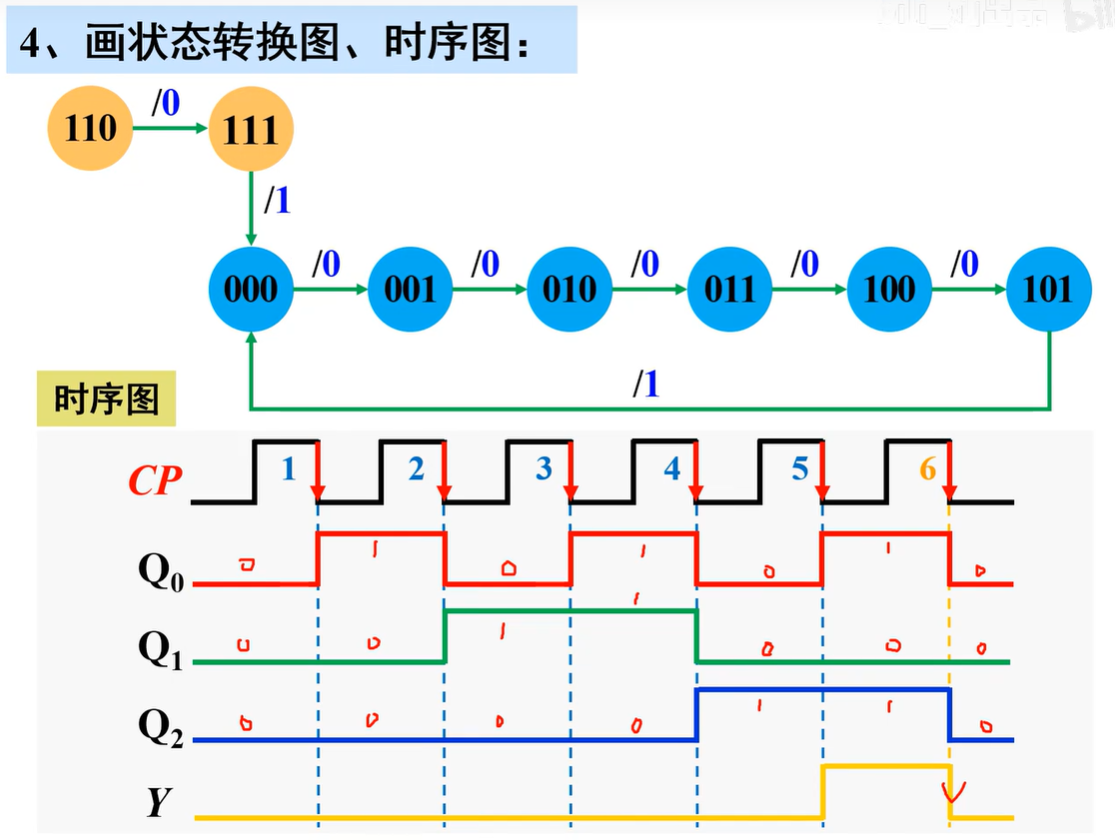
画状态转换图、时序图:
- 状态转换图:电路由现态转换到次态的示意图
- 时序图:在时钟脉冲CP作用下,各触发器状态变化的波形图
检查电路能否“自启动”:
- 能自启动:存在无效状态,但没有形成循环
- 不能自启动:存在无效状态,且形成了循环
电路功能说明:
- 逻辑功能:根据状态表或状态转换图来说明电路逻辑功能
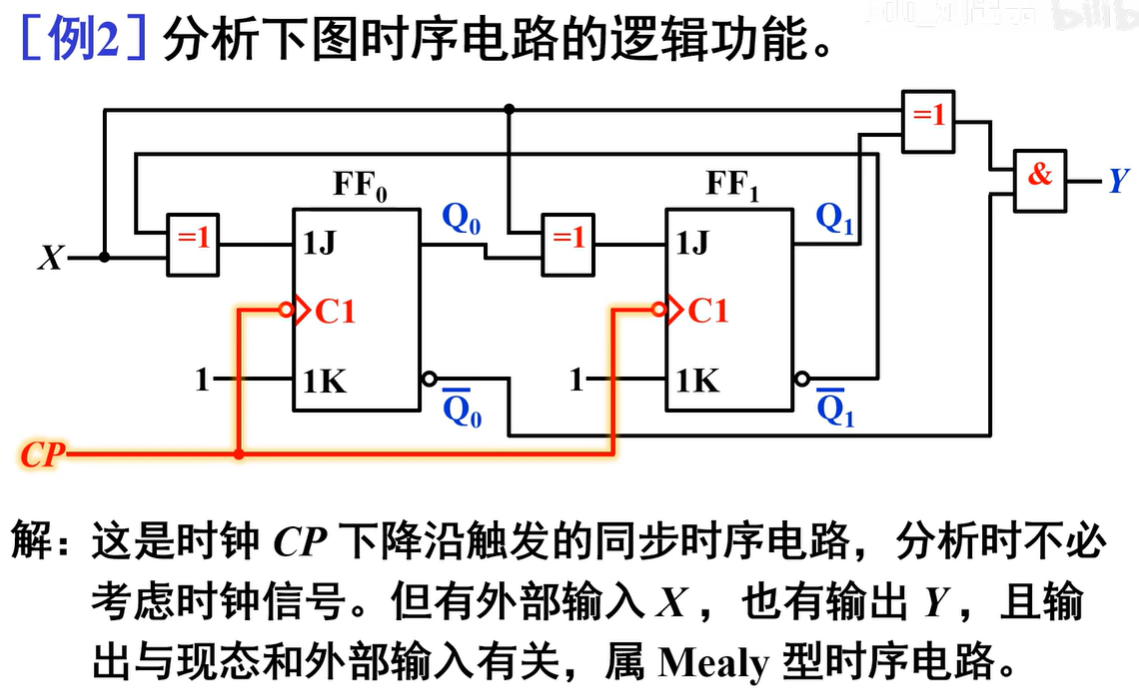
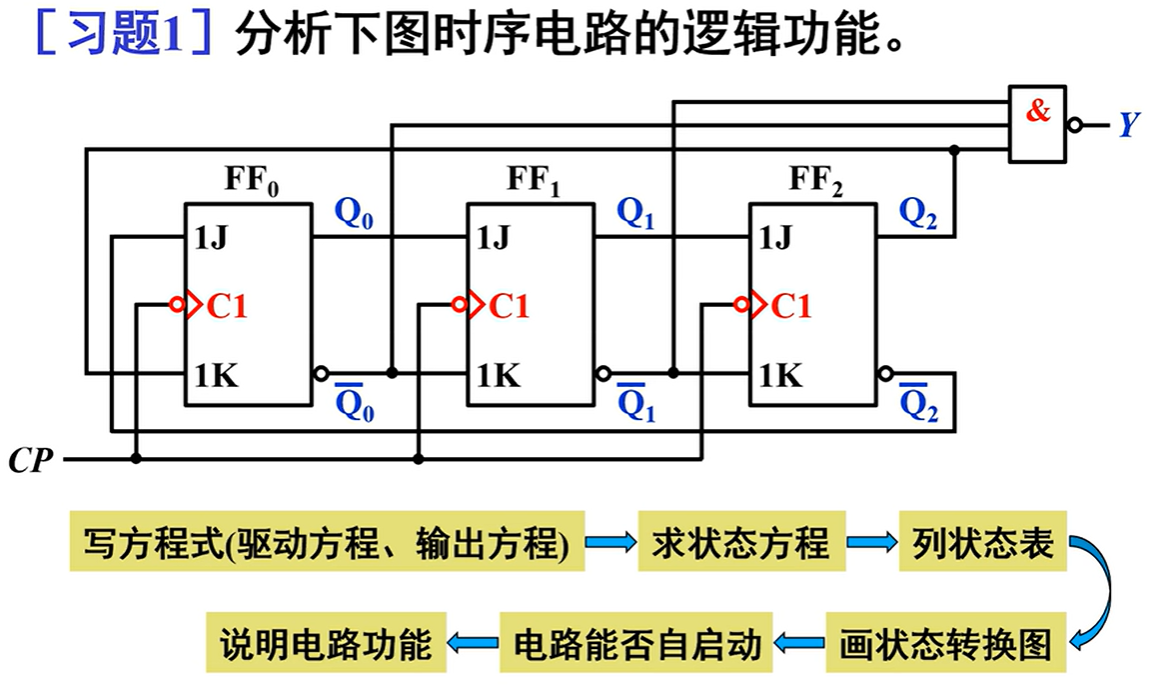
典例分析¶
驱动方程和输出方程都用现态\(Q^n\)表示,并且\(Q^n\)下标最好由大往小写,方便计算
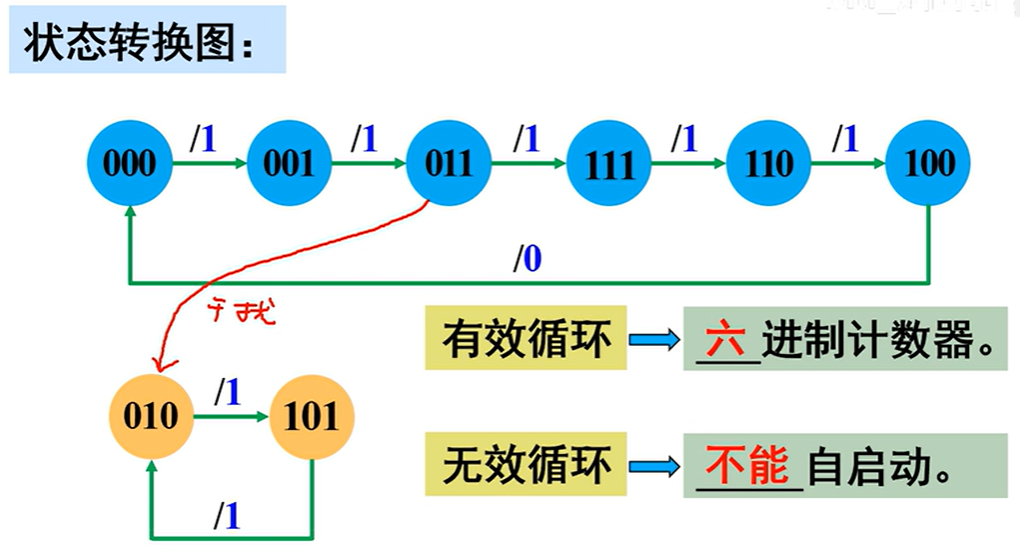
有效状态
- 被利用的状态:000、001、010、011、100、101
- 有效状态构成的循环称为“有效循环”
无效状态
- 没有被利用的状态:110、111
- 无效状态若构成循环称为“无效循环”
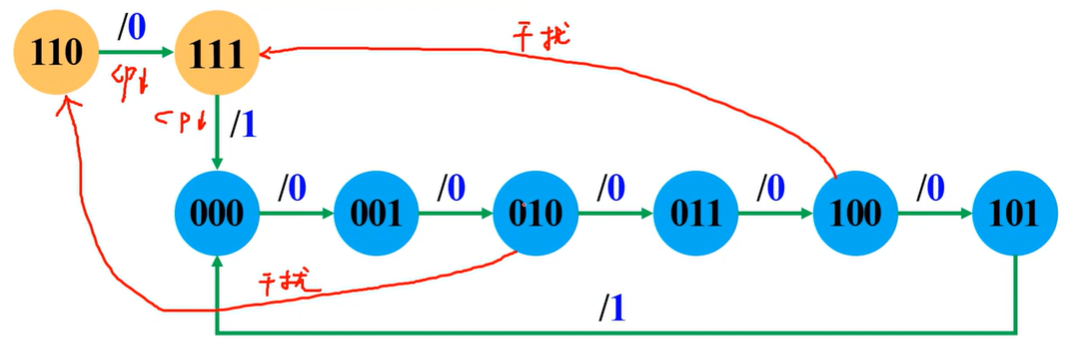
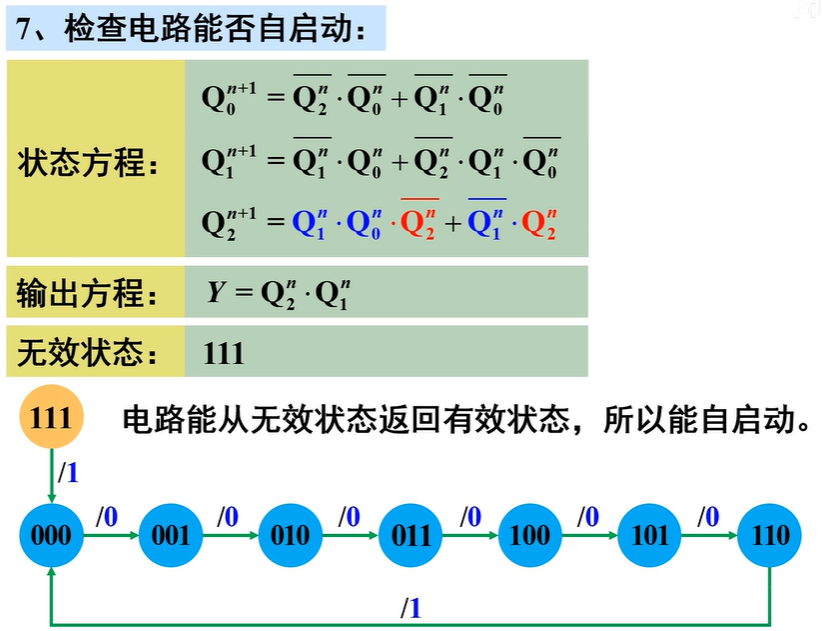
检查电路能否“自启动”
电路虽然存在无效状态,但没有形成循环,所以电路能自启动。即使电路由于某种原因进去无效状态,只要给足够的脉冲,就能返回到有效循环
其实指的就是如下图电路一样,即使受到干扰能否通过加脉冲的方式回到有效循环
电路功能说明
该电路能对CP脉冲进行六进制计数,并在Y端输出一个下降沿作为进位输出信号,为“同步六进制计数器”
化简会用到的公式
-
\(0\oplus A=A\)
-
\(1\oplus A=\bar A\)
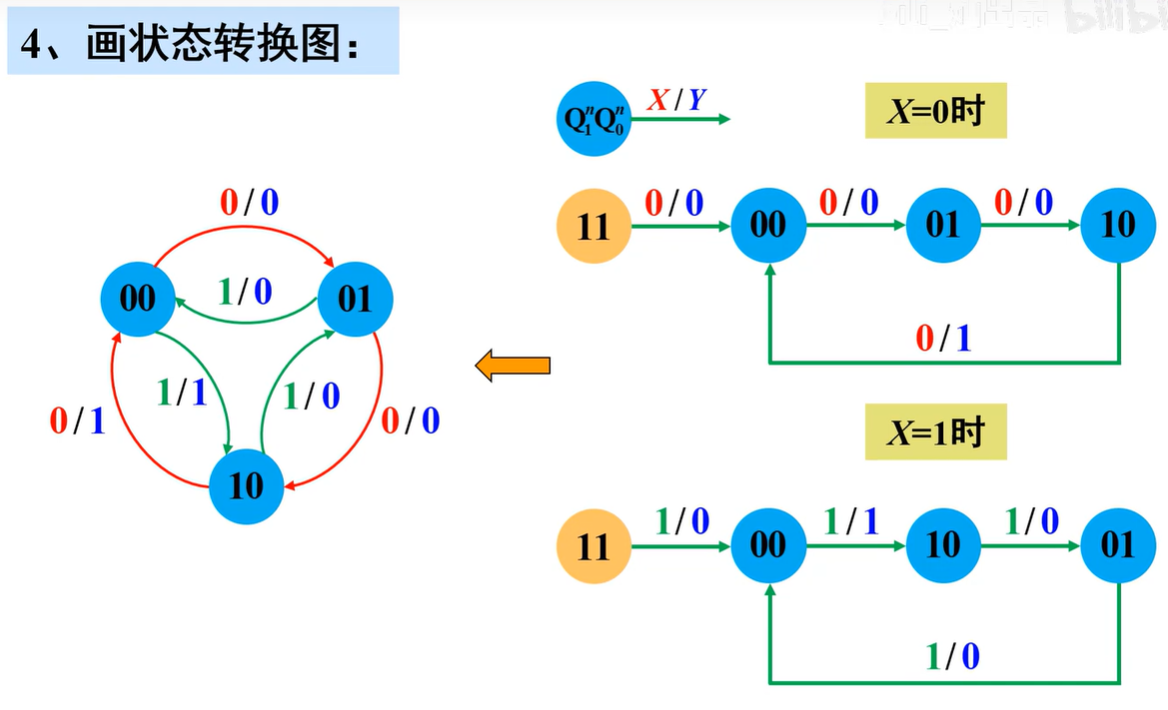
则当\(X=0\)时
- \(Q^{n+1}_{0}=(X\oplus \bar Q^{n}_{1})\cdot \bar Q^{n}_{0}=\bar Q^{n}_{1}\cdot \bar Q^{n}_{0}\)
-
\(Q^{n+1}_{1}=(X\oplus Q^{n}_{0})\cdot \bar Q^{n}_{1}=\bar Q^{n}_{1}\cdot Q^{n}_{0}\)
-
\(Y=(X\oplus Q^{n}_{1})\cdot \bar Q^{n}_{0}=Q^{n}_{1}\cdot \bar Q^{n}_{0}\)
当\(X=1\)时
- \(Q^{n+1}_{0}=(X\oplus \bar Q^{n}_{1})\cdot \bar Q^{n}_{0}=Q^{n}_{1}\cdot \bar Q^{n}_{0}\)
-
\(Q^{n+1}_{1}=(X\oplus Q^{n}_{0})\cdot \bar Q^{n}_{1}=\bar Q^{n}_{1}\cdot \bar Q^{n}_{0}\)
-
\(Y=(X\oplus Q^{n}_{1})\cdot \bar Q^{n}_{0}=\bar Q^{n}_{1}\cdot \bar Q^{n}_{0}\)
其实就是在\(X=0\)时是一个三进制加法器,\(Y=1\)代表进位;在\(X=1\)时是一个三进制减法器,\(Y=1\)代表借位
电路功能说明
该电路是一个受输入X控制的三进制可逆计数器(既可以加法也可以减法),且能自启动
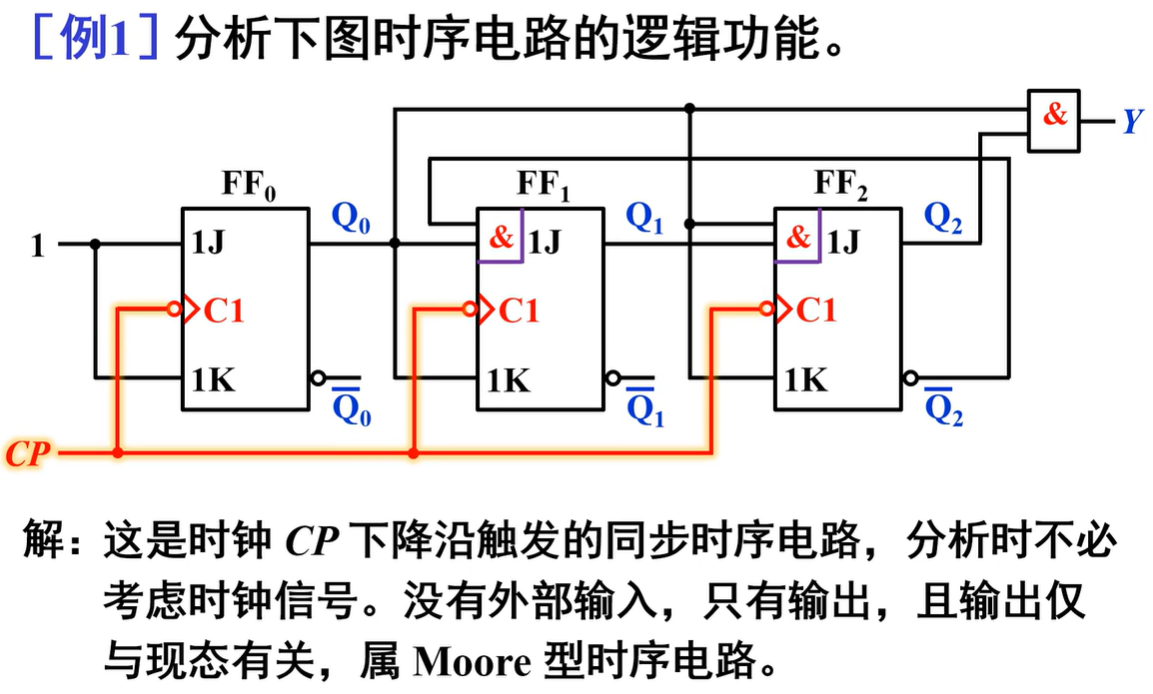
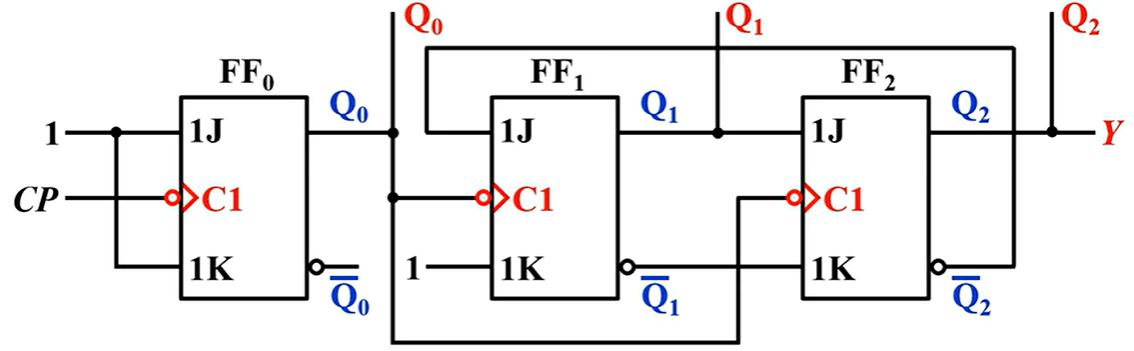
异步时序电路的分析方法¶
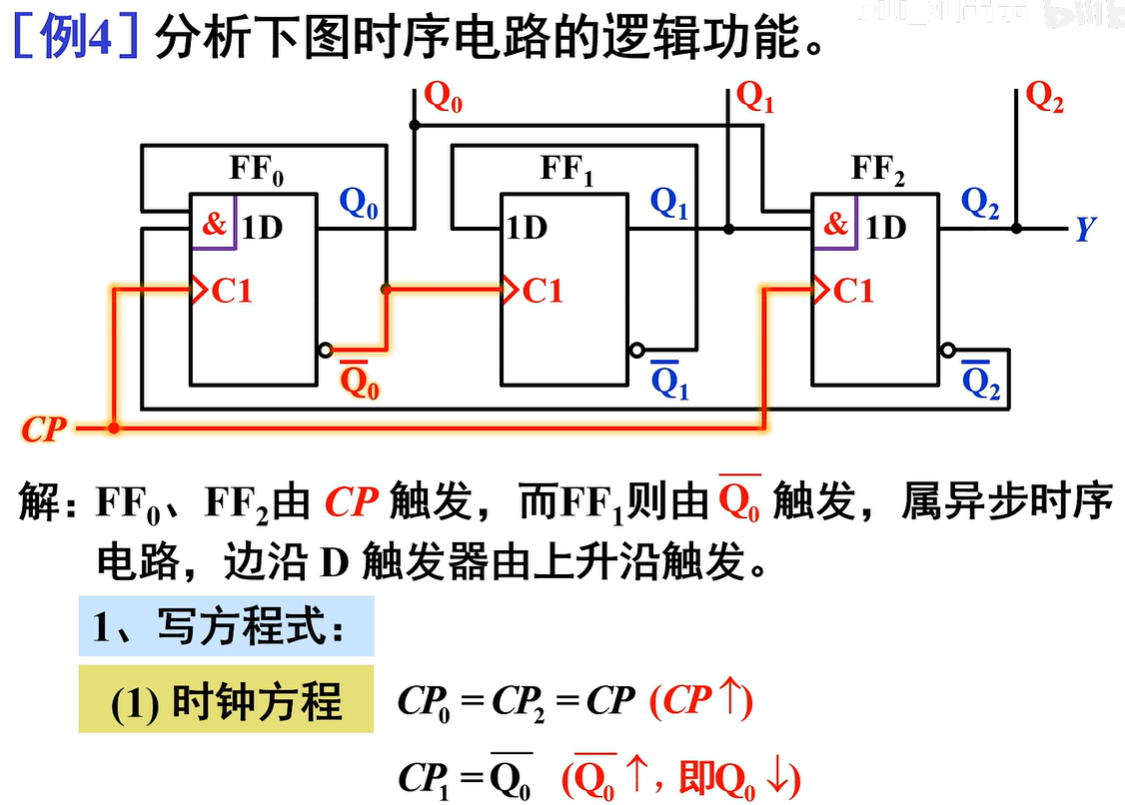
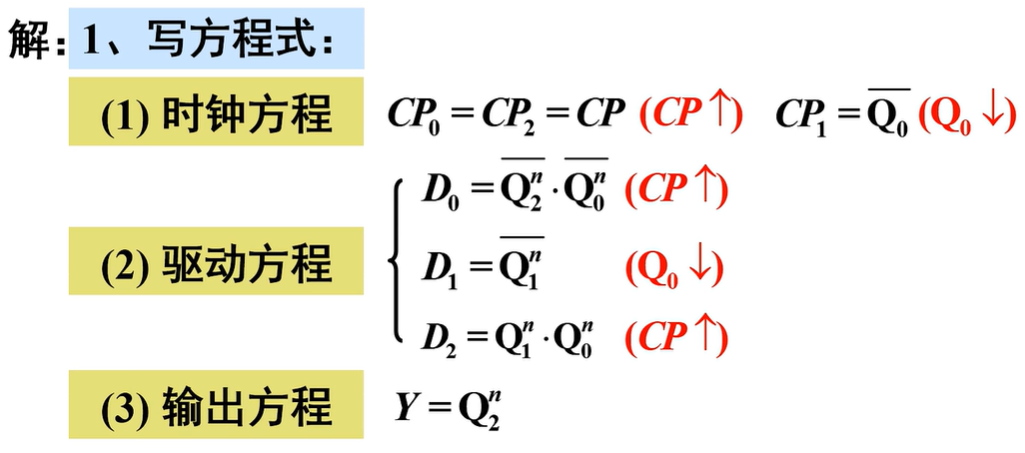
在异步时序电路中,只有部分触发器由时钟脉冲CP触发,其他触发器由电路内部信号触发。分析异步时序电路时需写出时钟方程,并特别注意各触发器的时钟条件在何时满足,其状态方程才能使用
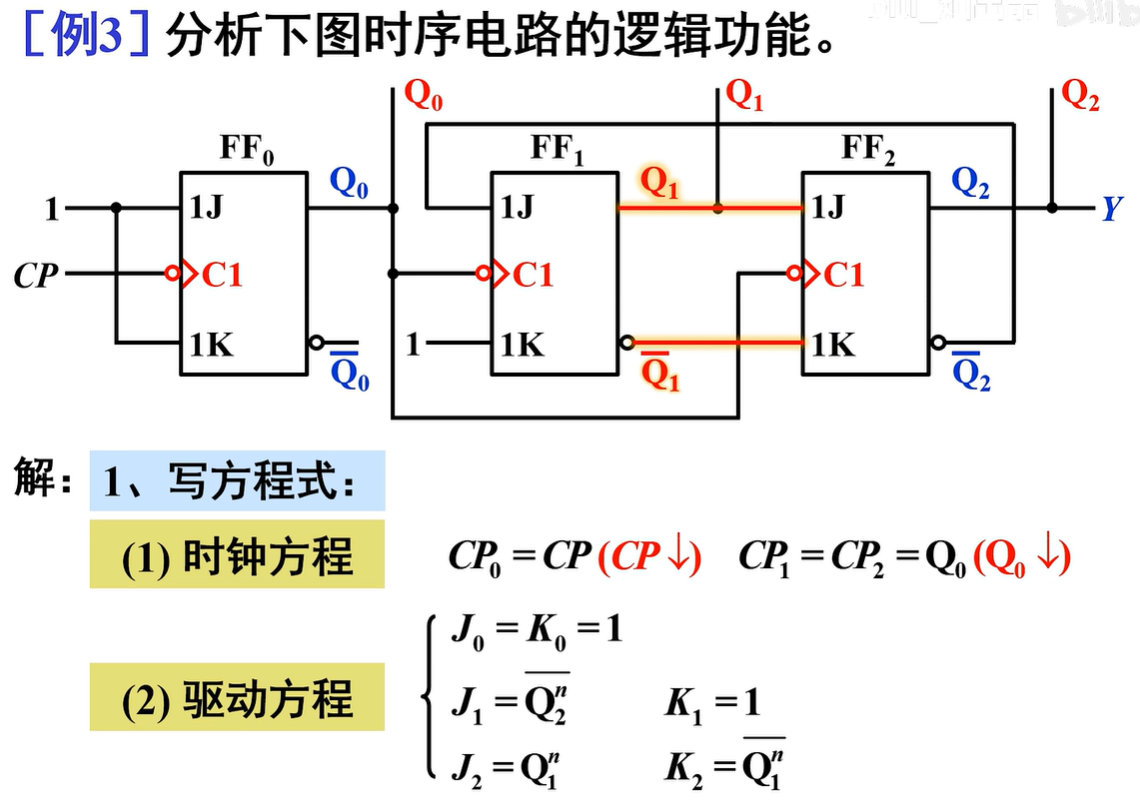
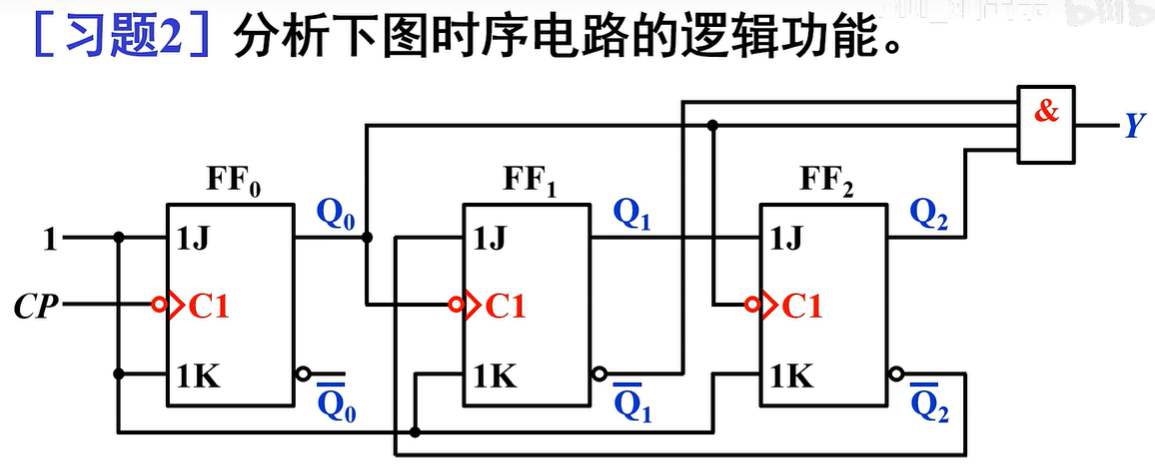
\(FF_0\)由CP触发,而\(FF_1\)、\(FF_2\)则由\(Q_0\)触发,故为异步时序电路
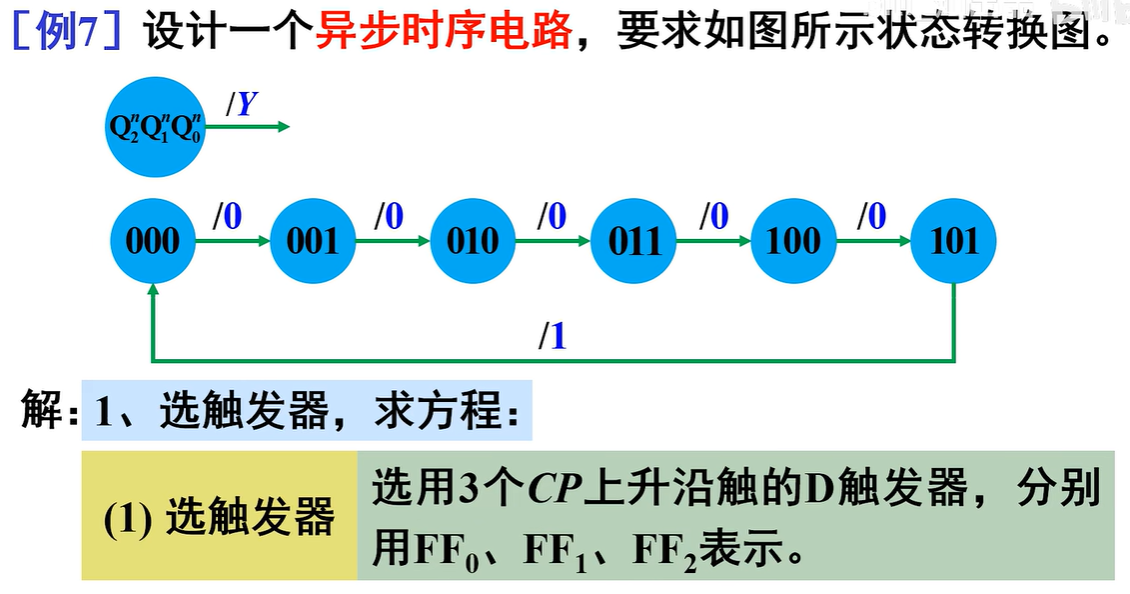
典例分析¶
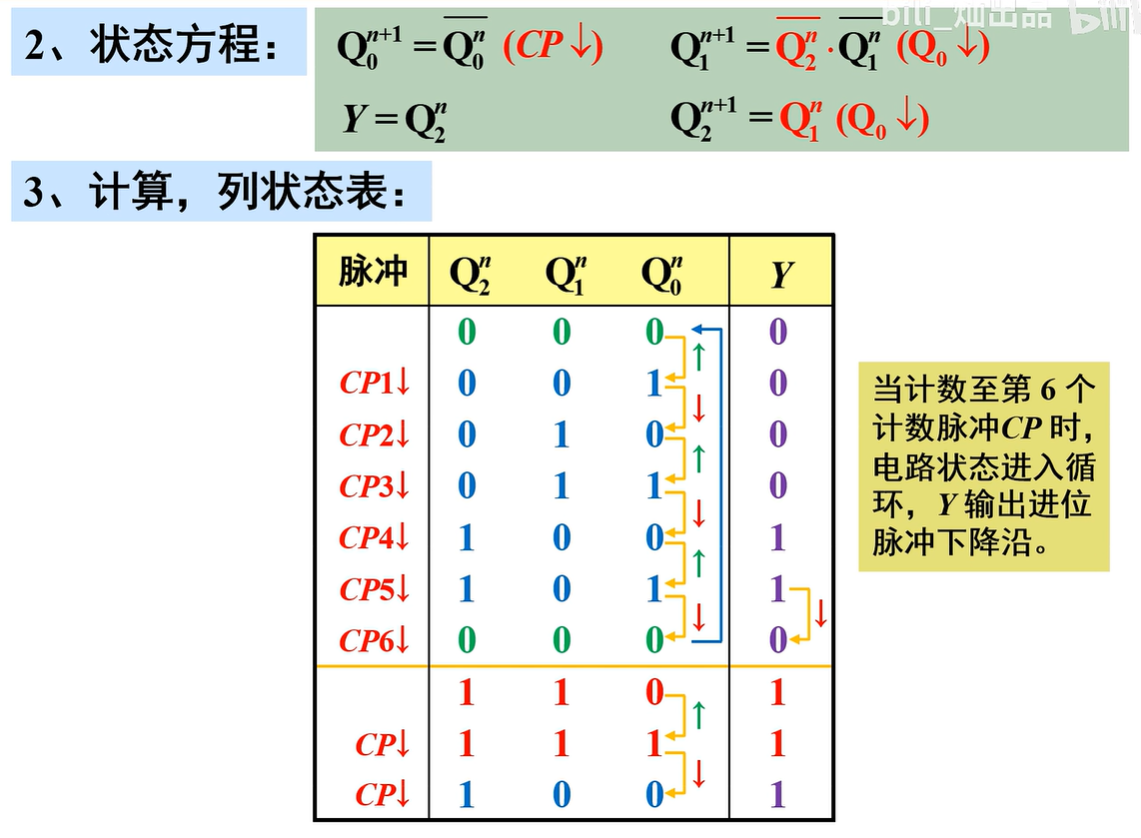
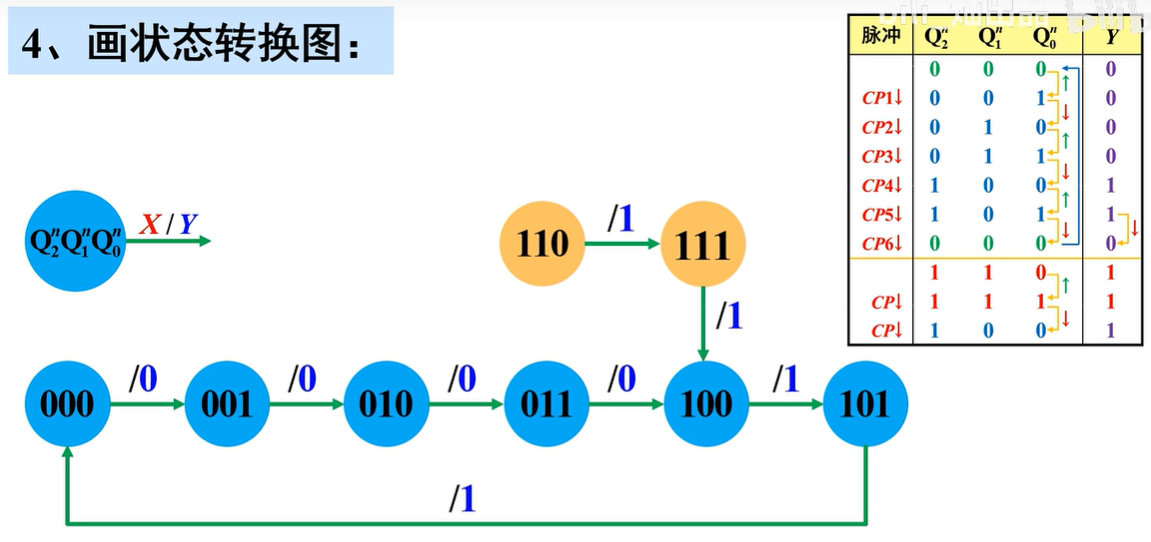
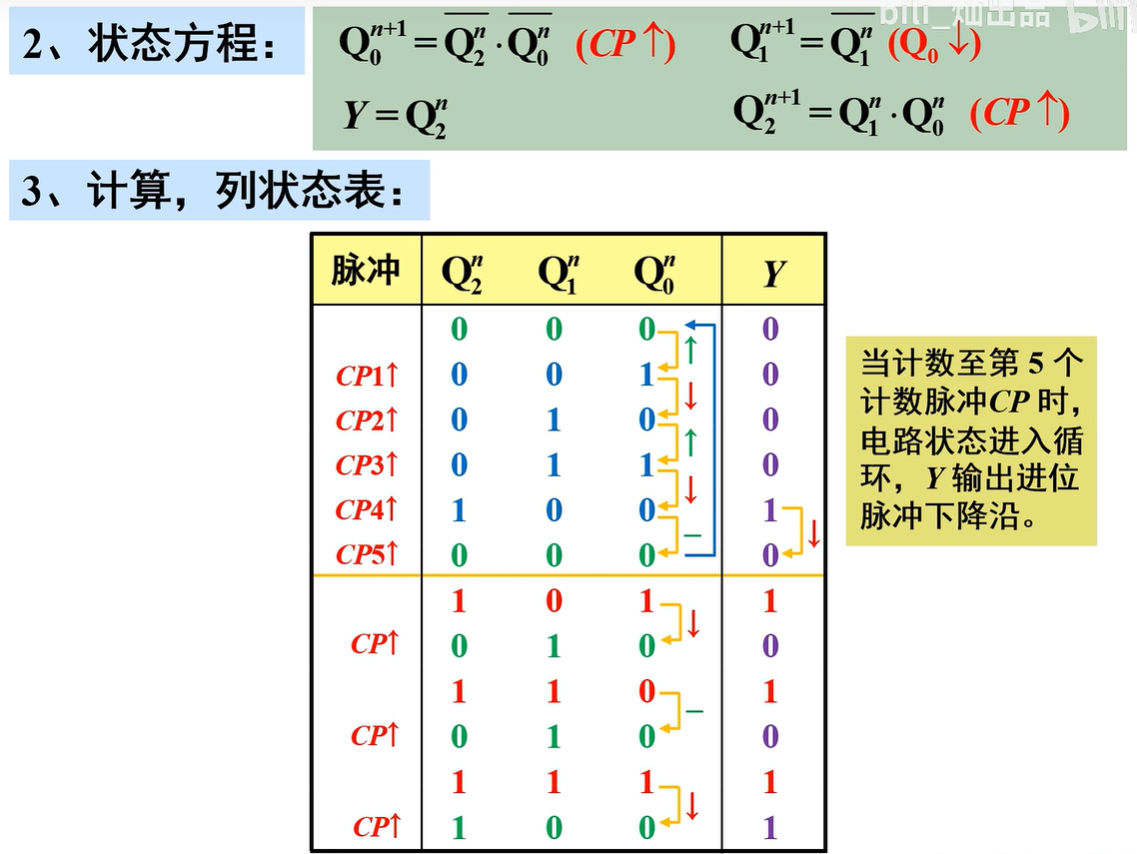
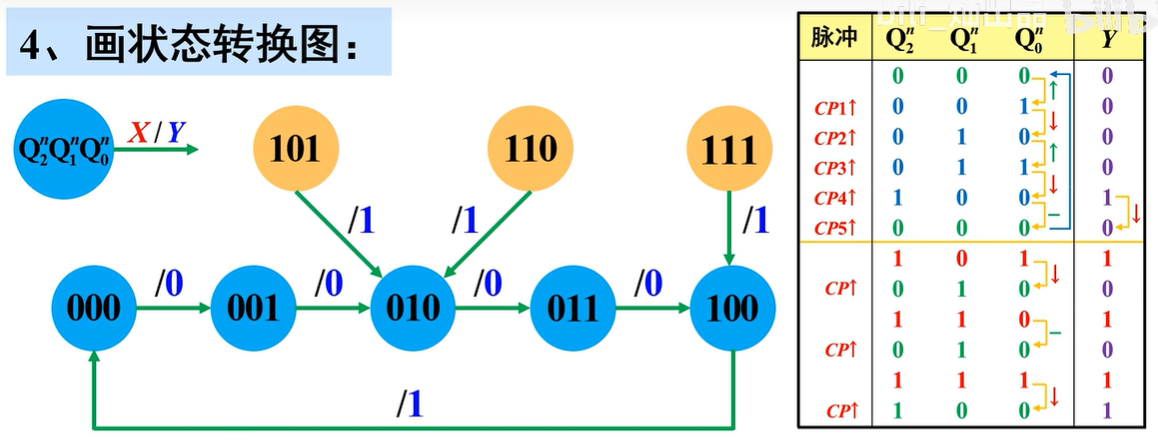
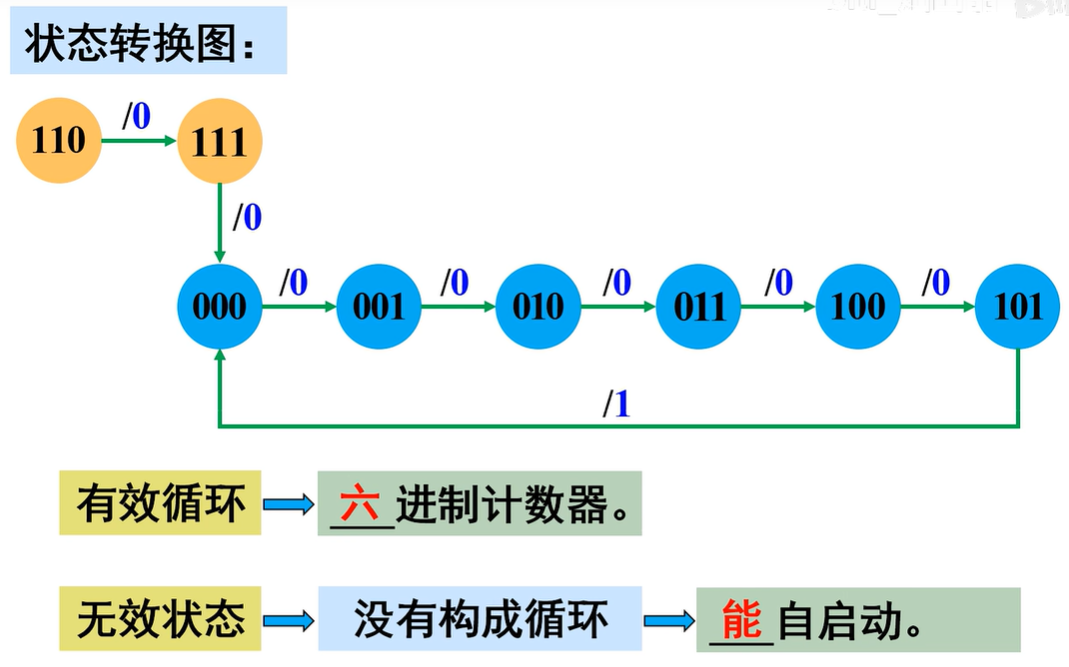
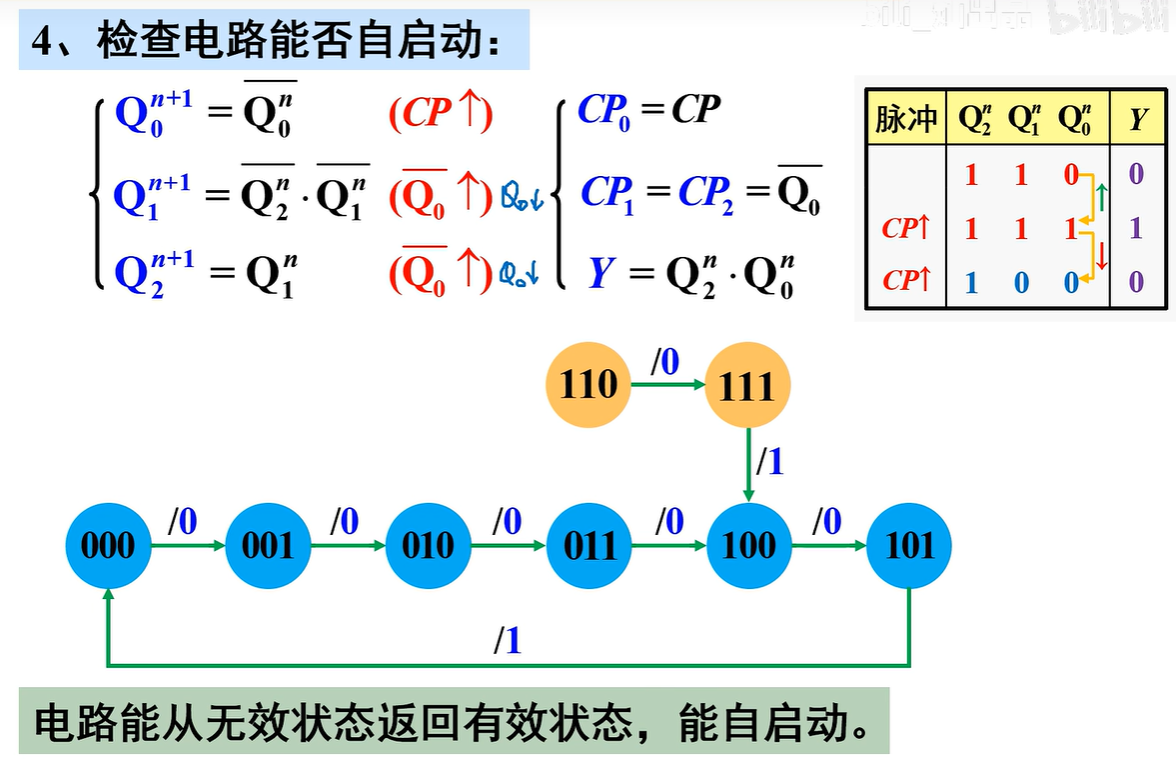
检查电路能否“自启动”
电路存在无效状态,但没有形成循环,所以电路能自启动
电路功能说明
该电路能对CP脉冲进行六进制计数,并在Y端输出一个下降沿作为进位输出信号,为“异步六进制计数器”
检查电路能否“自启动”
电路存在无效状态,但没有形成循环,所以电路能自启动
电路功能说明
该电路能对CP脉冲进行五进制计数,并在Y端输出一个下降沿作为进位输出信号,为“异步五进制计数器”
时序电路的设计¶
同步时序电路的设计¶
基本步骤¶
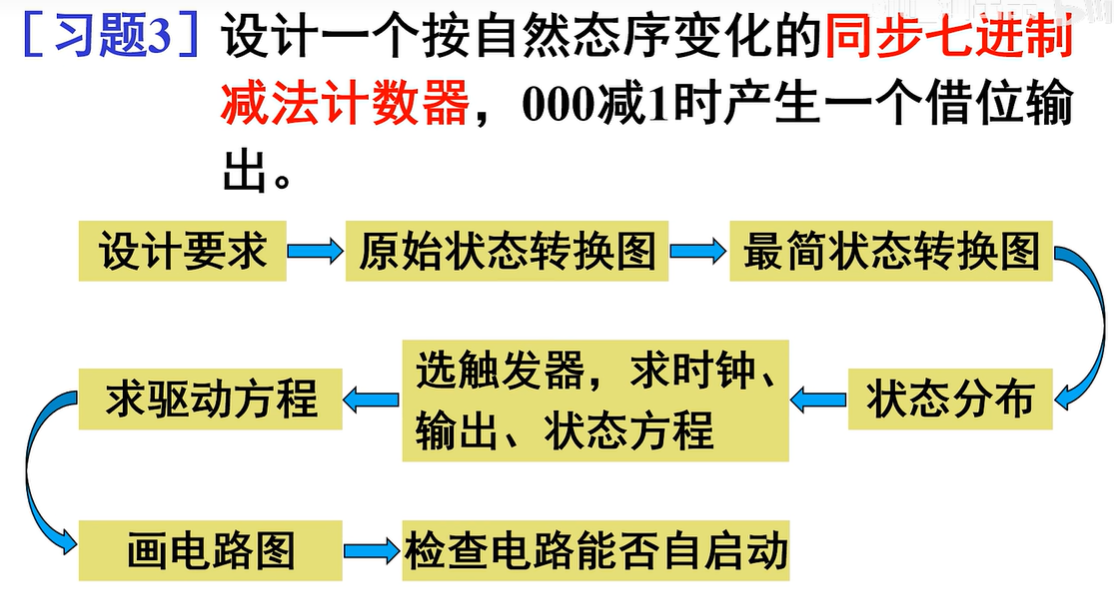
设计要求\(\longrightarrow\)原始状态转换图\(\longrightarrow\)最简状态转换图\(\longrightarrow\)状态分布\(\longrightarrow\)选触发器,求时钟、输出、状态方程 \(\longrightarrow\)求驱动方程\(\longrightarrow\)画电路图\(\longrightarrow\)检查电路能否自启动
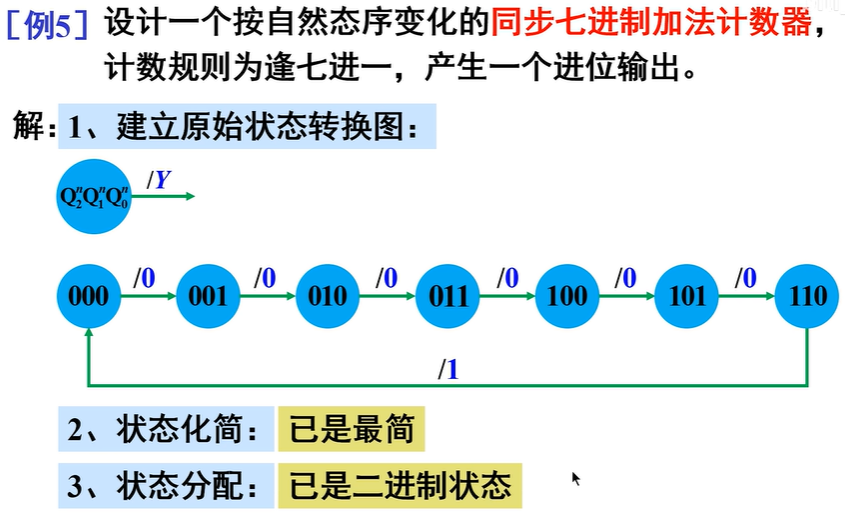
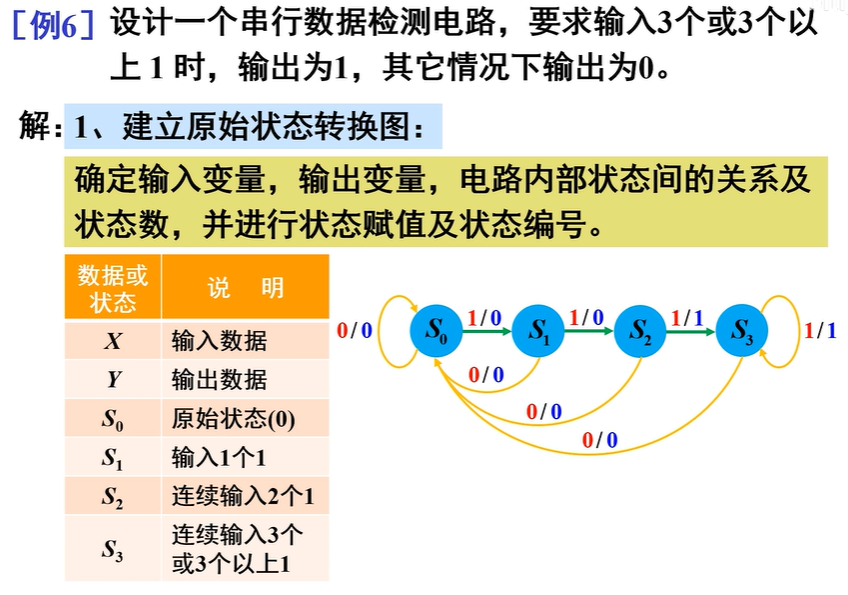
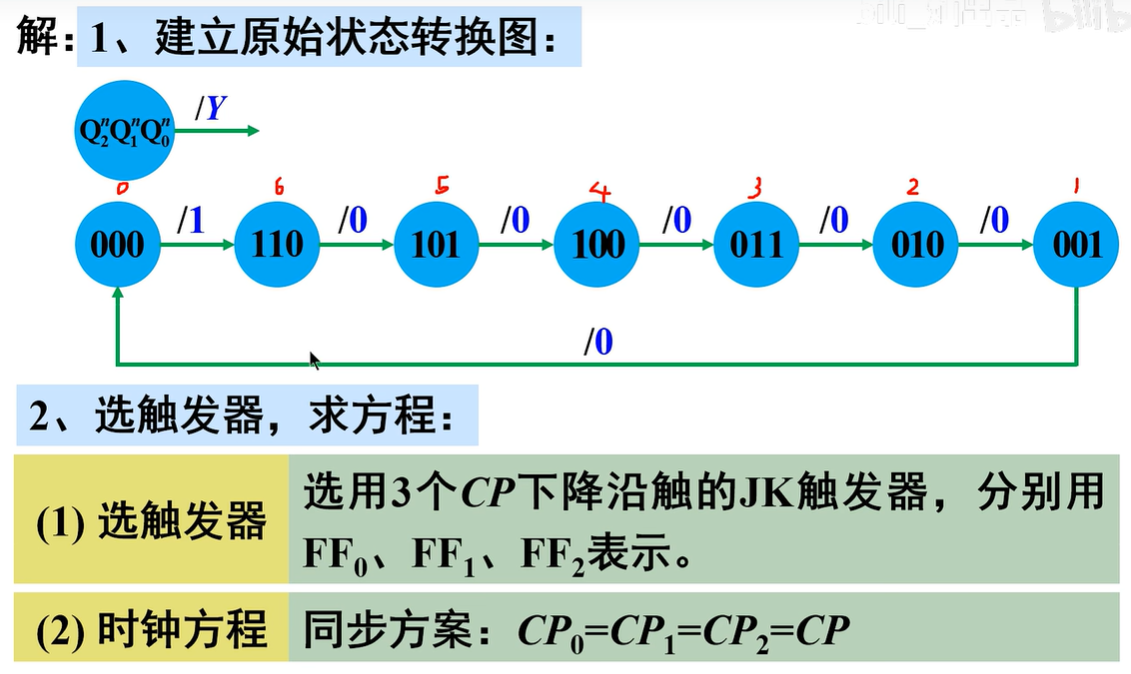
典例分析¶
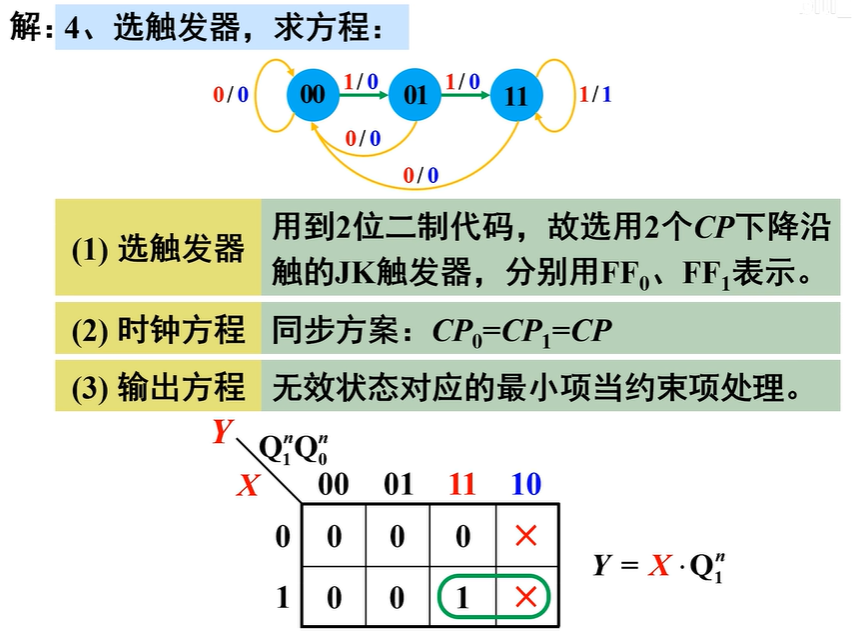
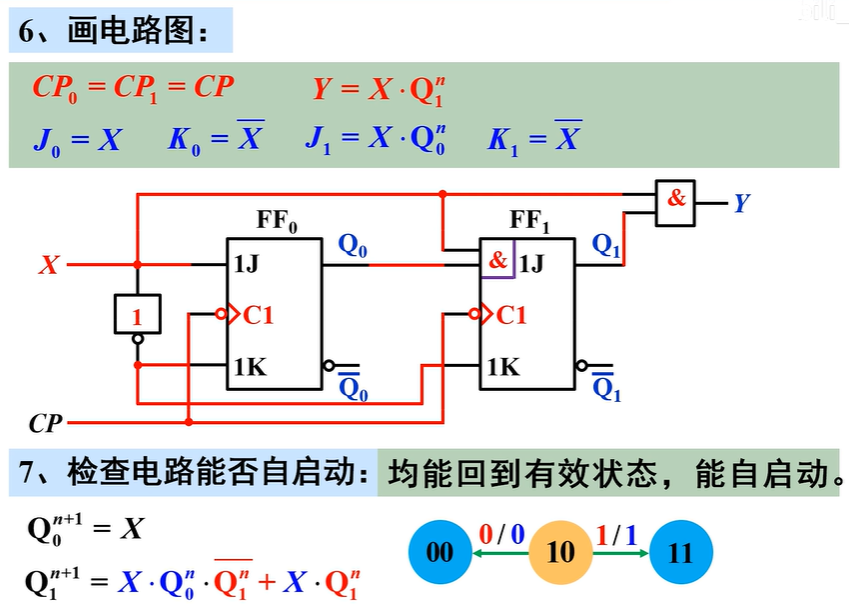
选触发器,求方程
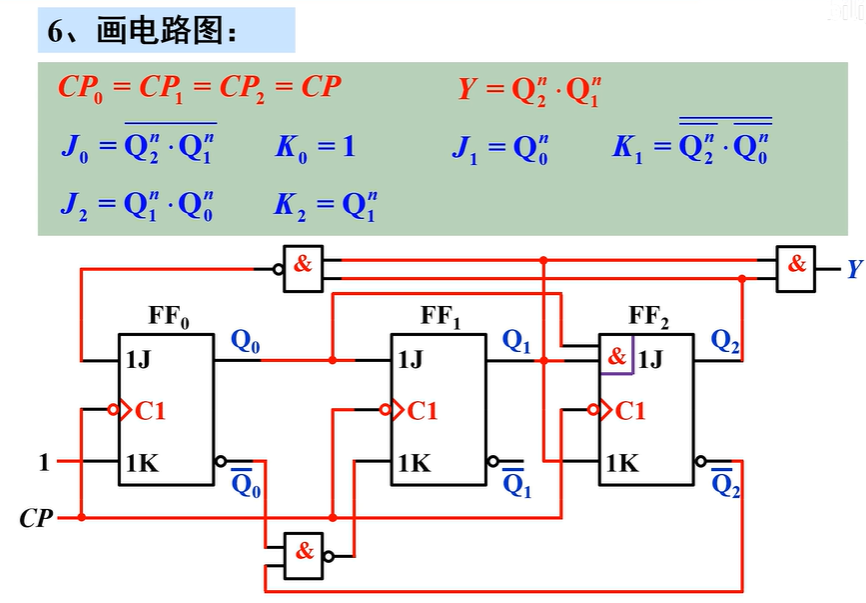
- 选触发器:用到3位二进制代码,故选用3个CP下降沿触发的JK触发器,分别用\(FF_0\)、\(FF_1\)、\(FF_2\)表示
- 时钟方程:同步方案\(CP_0=CP_1=CP_2=CP\)
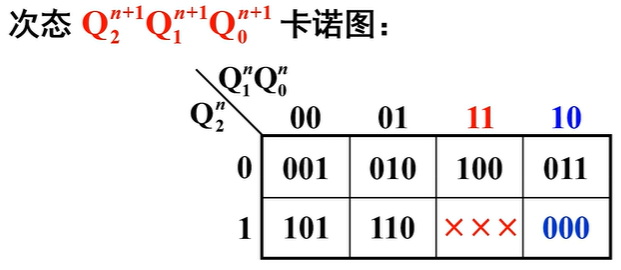
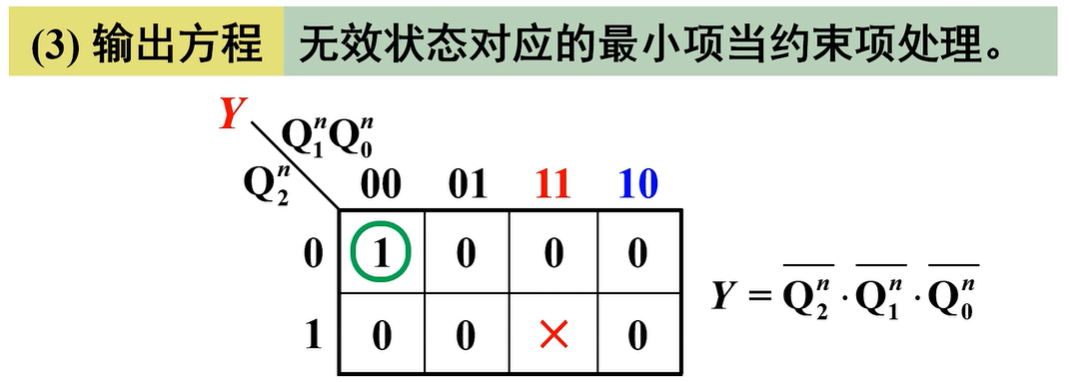
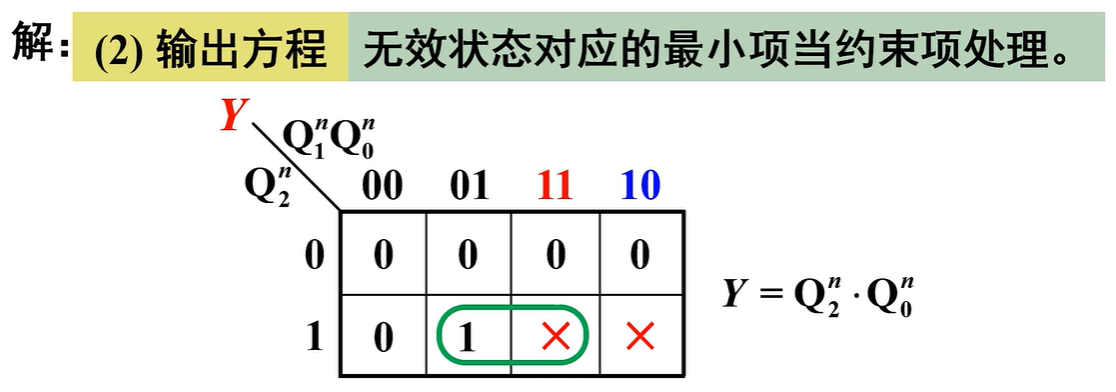
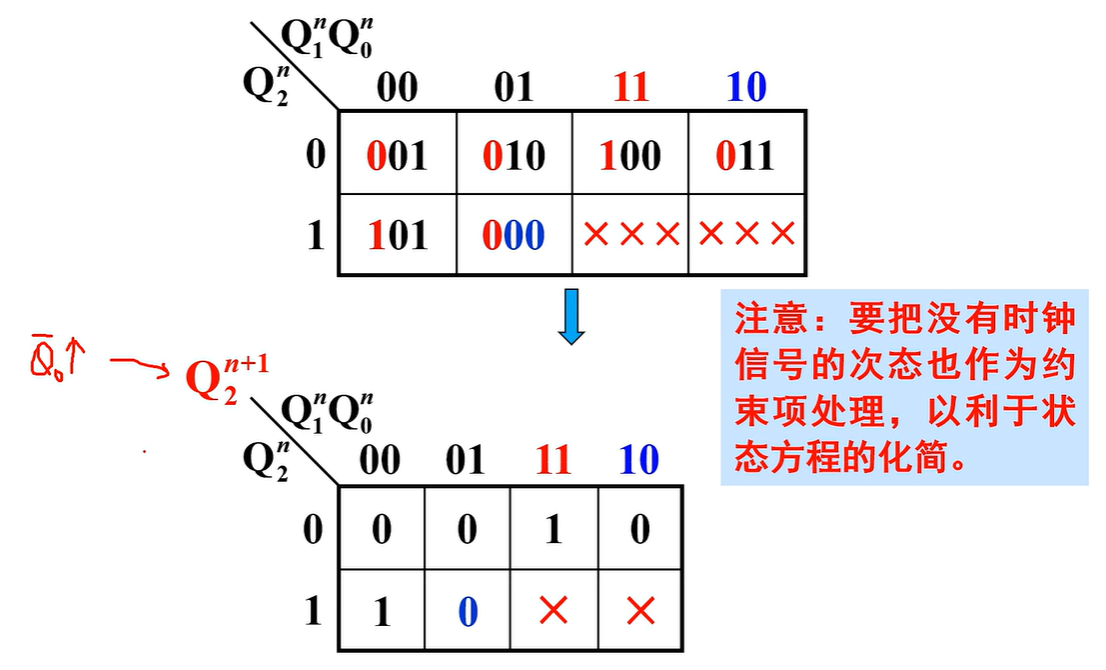
- 输出方程:无效状态对应的最小项当约束项处理
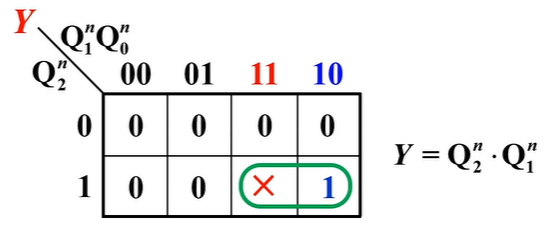
输出方程
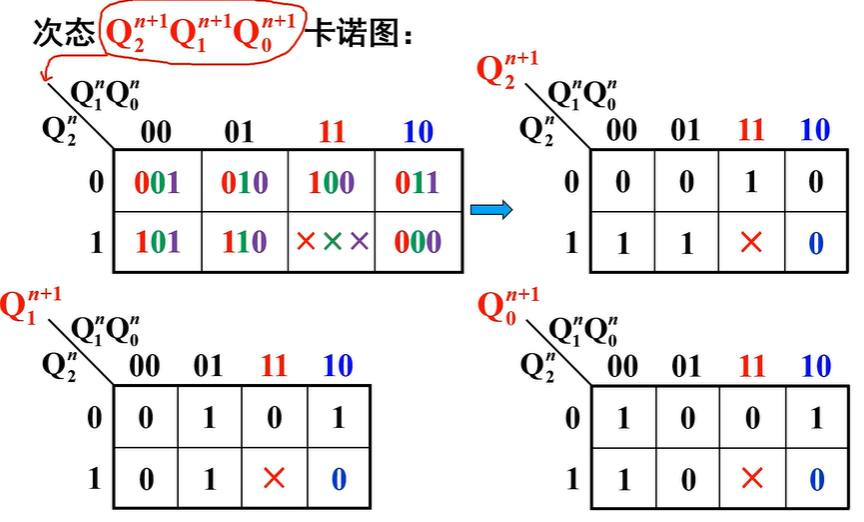
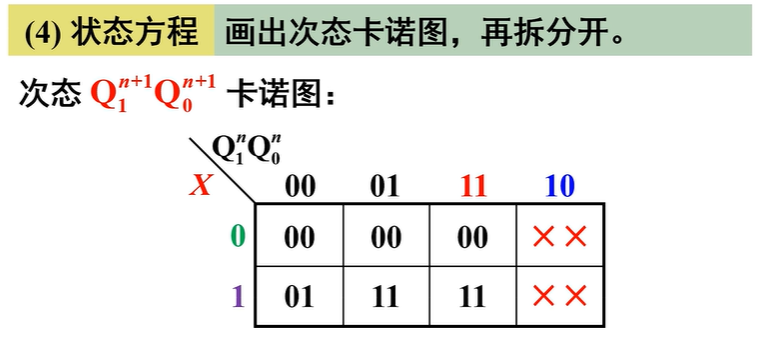
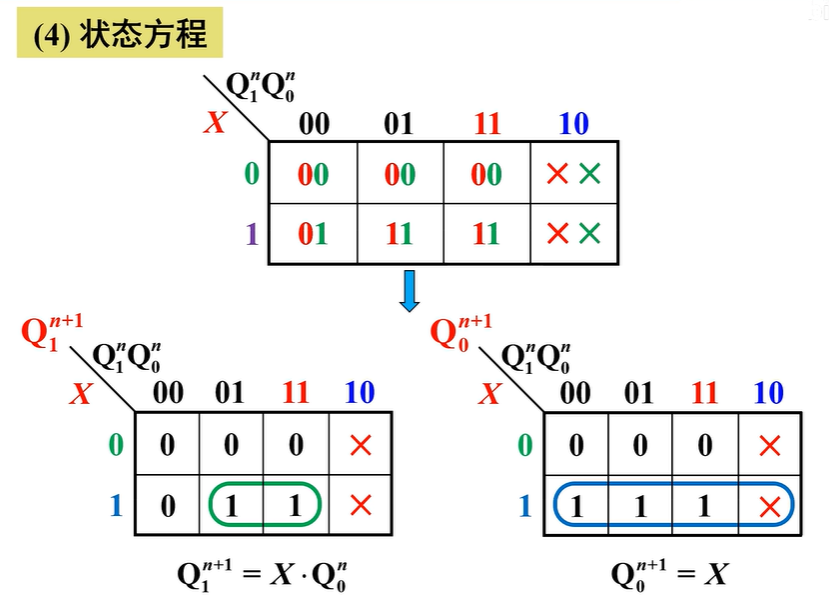
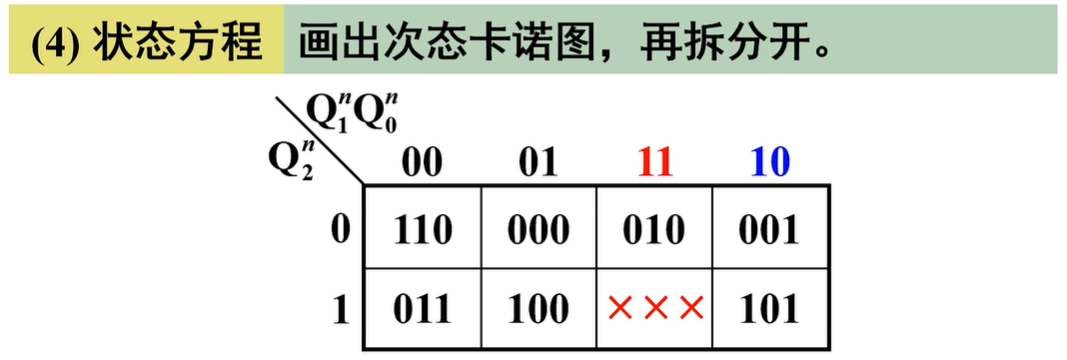
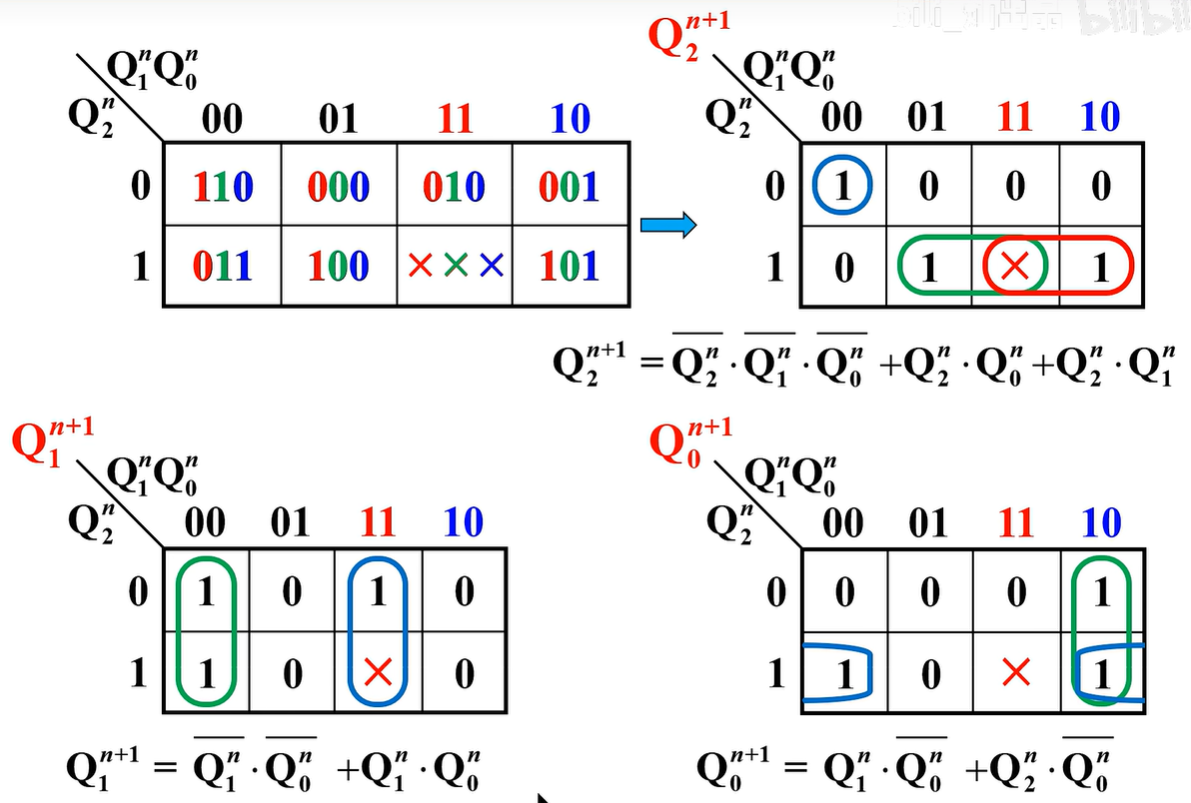
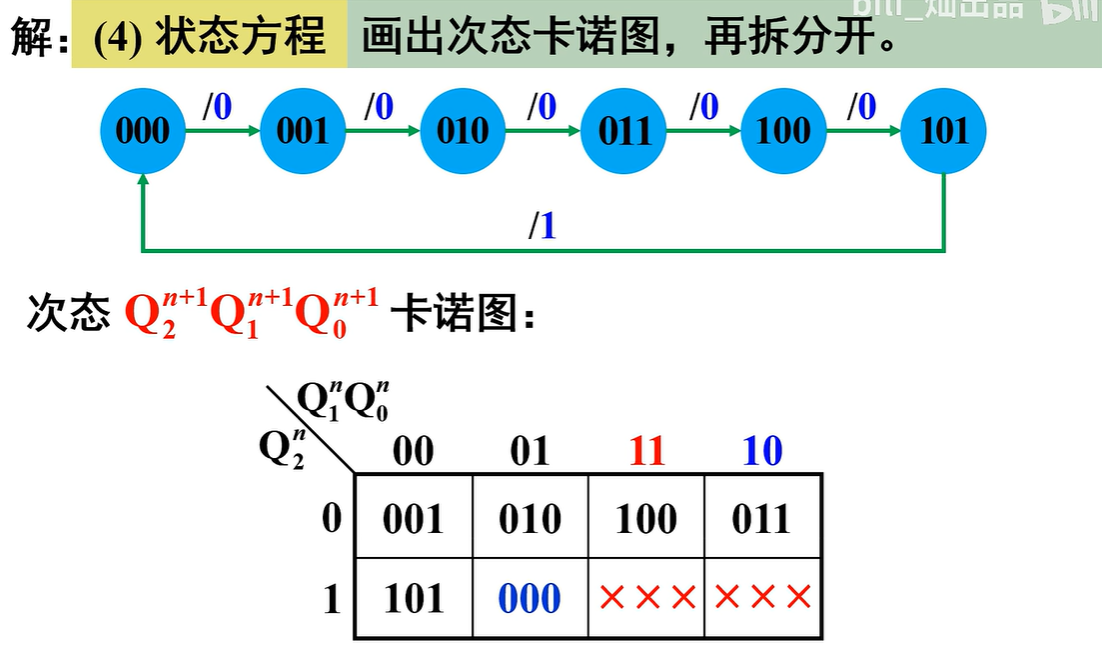
- 状态方程:先画出次态卡诺图(其实是就是看该现态状态对应的下一个状态是什么),再拆分开得各触发器卡诺图
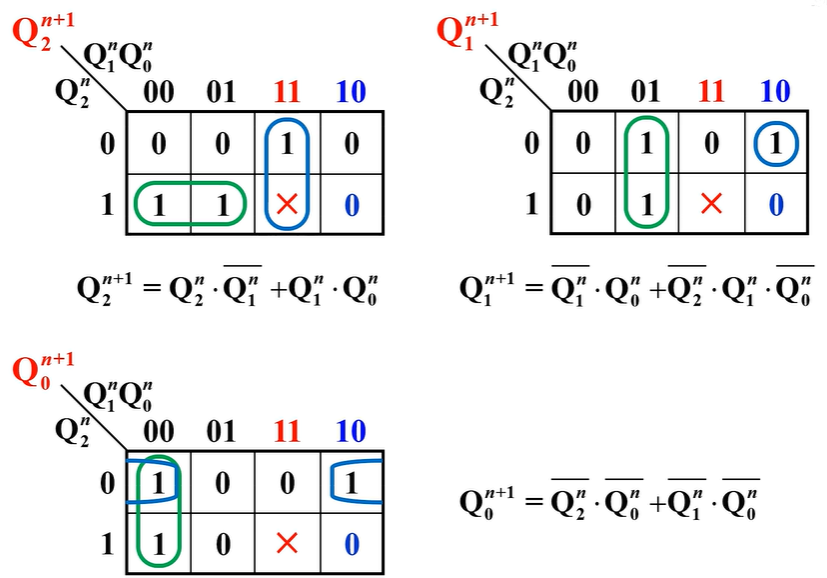
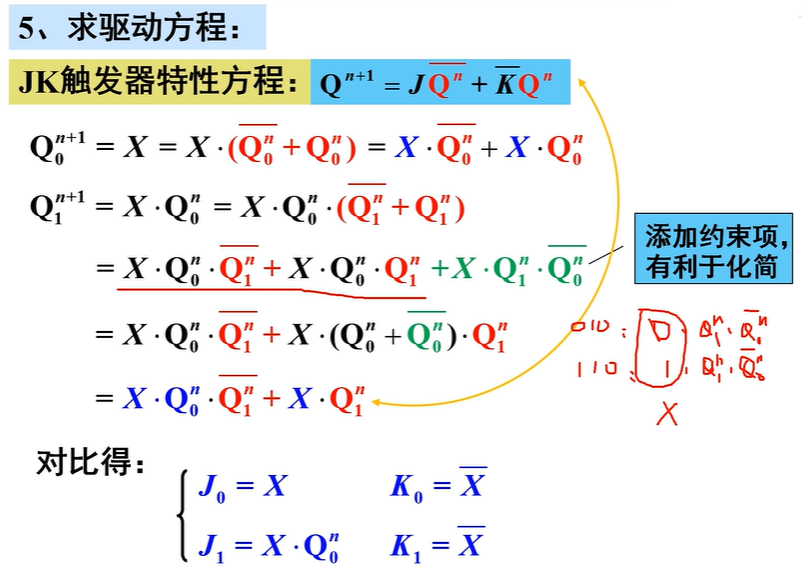
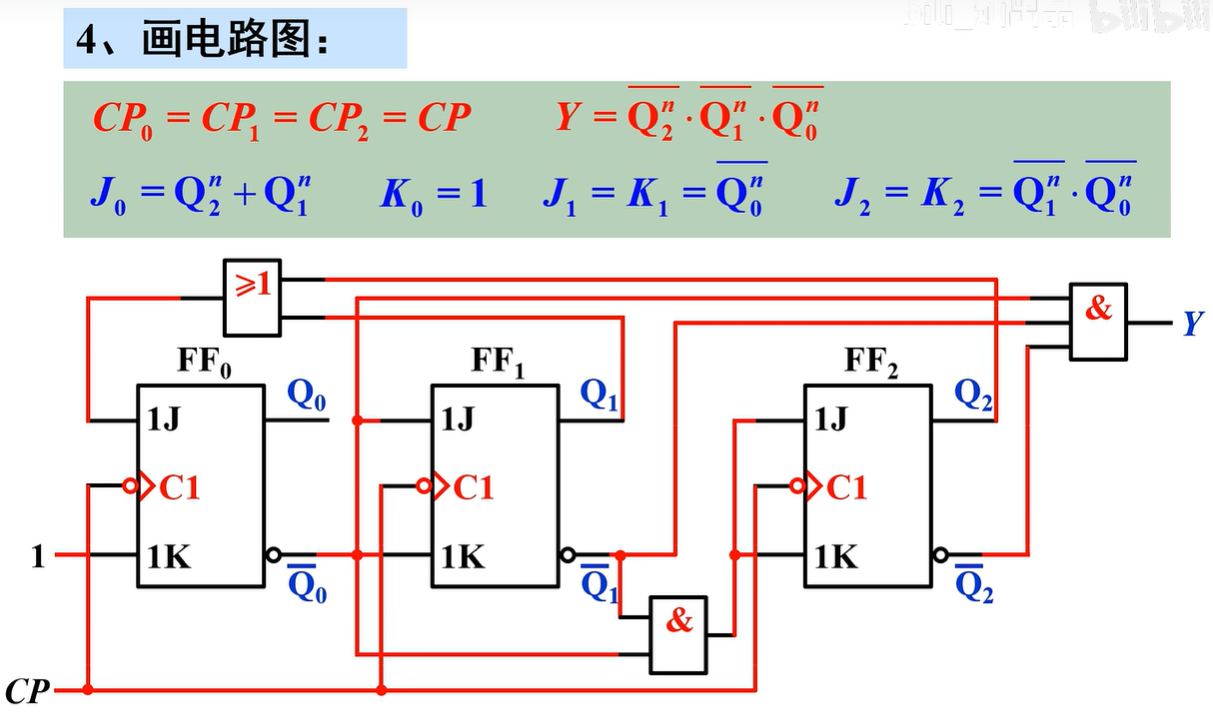
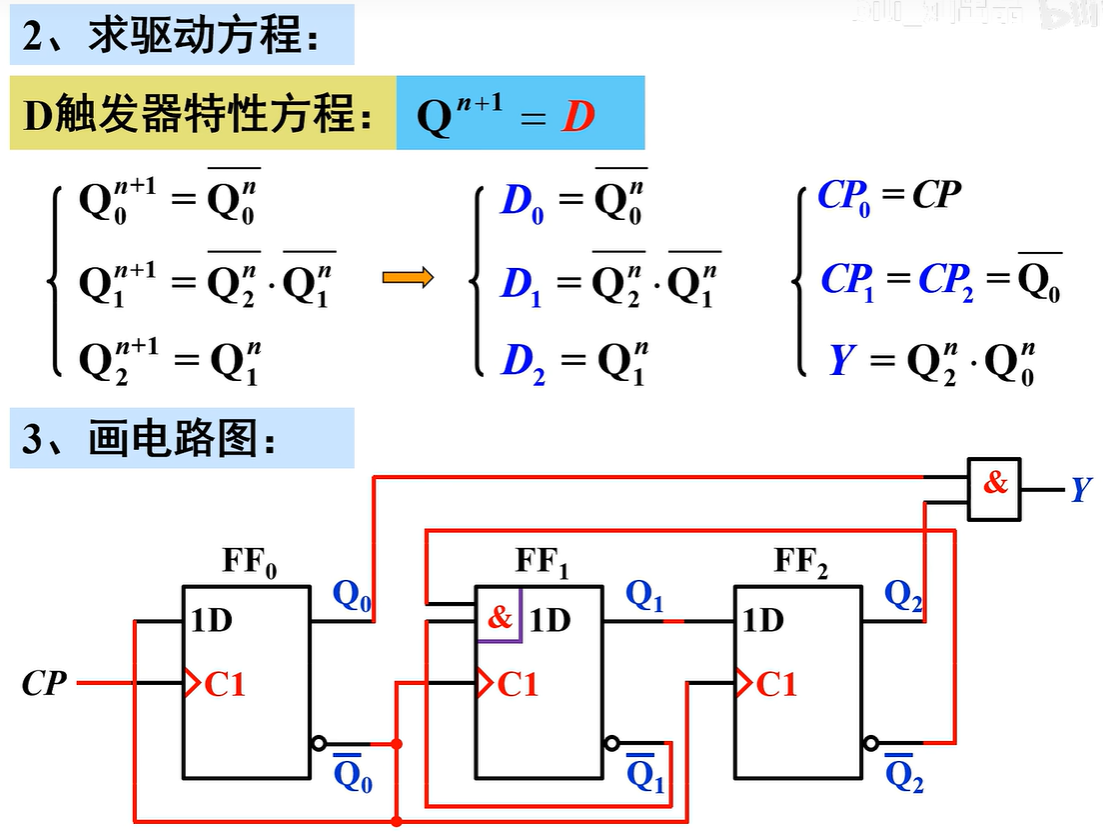
求驱动方程
变换状态方程,使之形式与选用触发器的特性方程一致,比较后得驱动方程
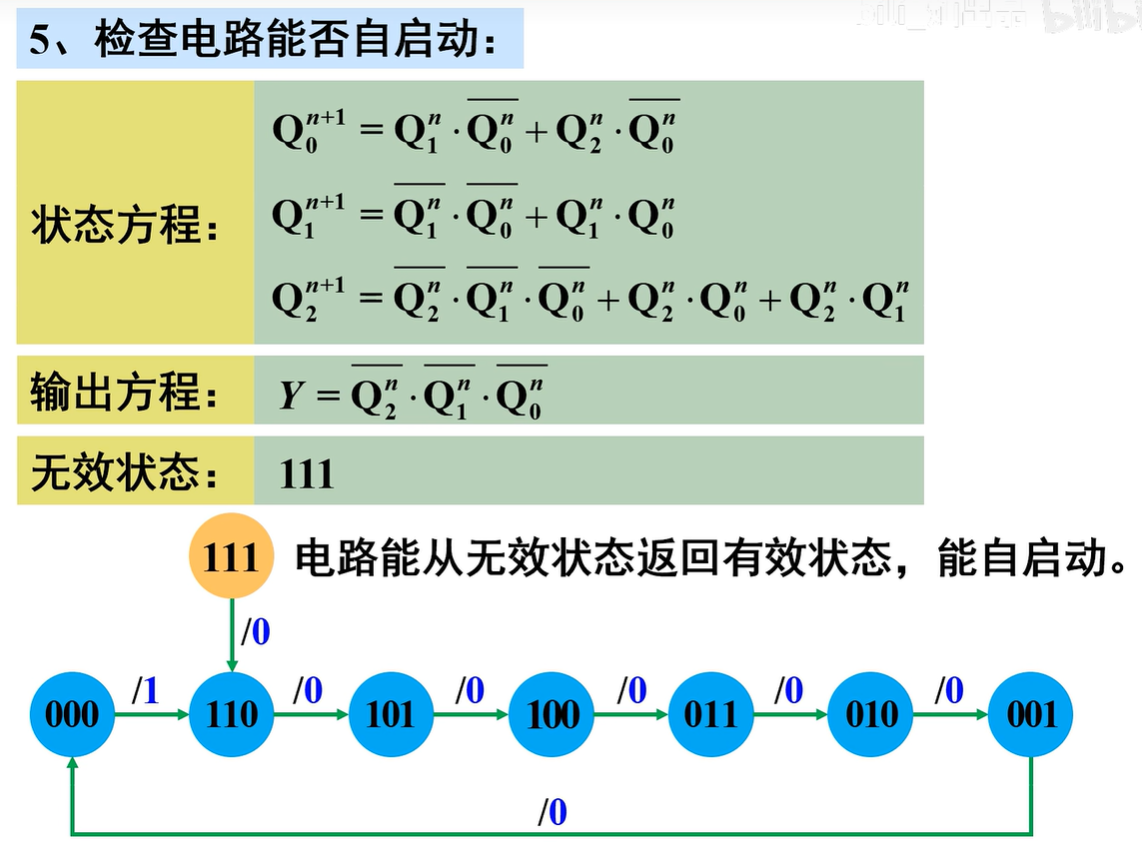
检查电路能否自启动时的状态方程\(Q^{n+1}_{2}\)要用\(Q^{n}_{1}\cdot Q^{n}_{0}\cdot \bar Q^n_{2}+\bar Q^n_1\cdot Q^n_2\)而不是\(Q^n_2 \cdot \bar Q^n_1+Q^{n}_{1}\cdot Q^{n}_{0}\)
,因为电路图是根据\(Q^{n}_{1}\cdot Q^{n}_{0}\cdot \bar Q^n_{2}+\bar Q^n_1\cdot Q^n_2\)方程得到的(把约束项当作0消去了约束项,所以二者方程结果会不同)
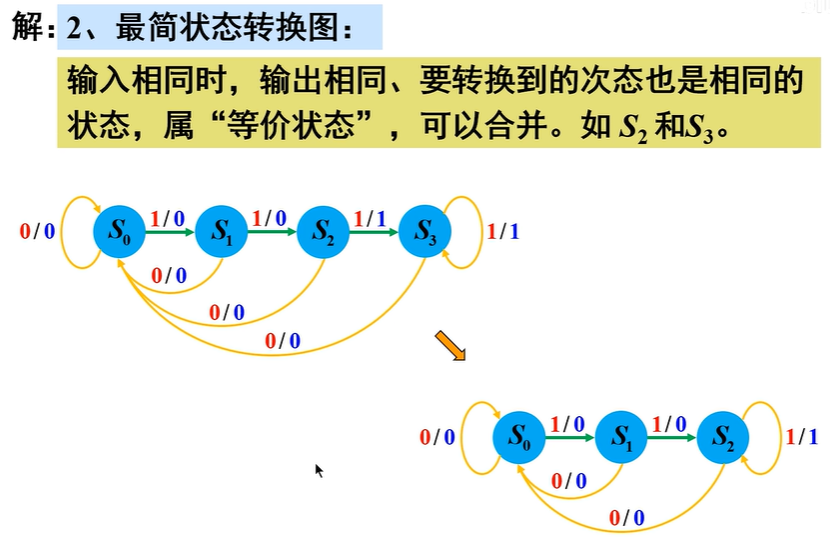
判断“等价状态”的方法:看输入相同时,输出、要转换到的次态是否相同
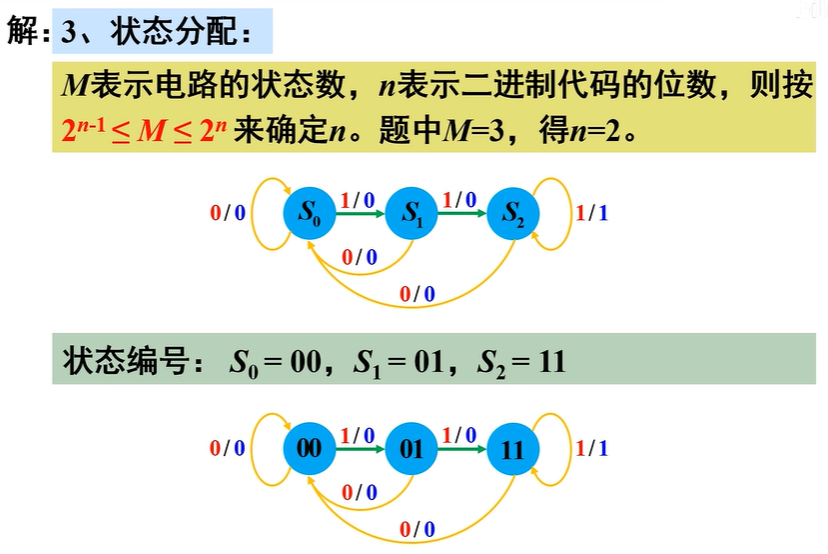
状态编号当然也可以用10,但是为了和题意更为贴近(输入1的个数)选用了11
异步时序电路的设计¶
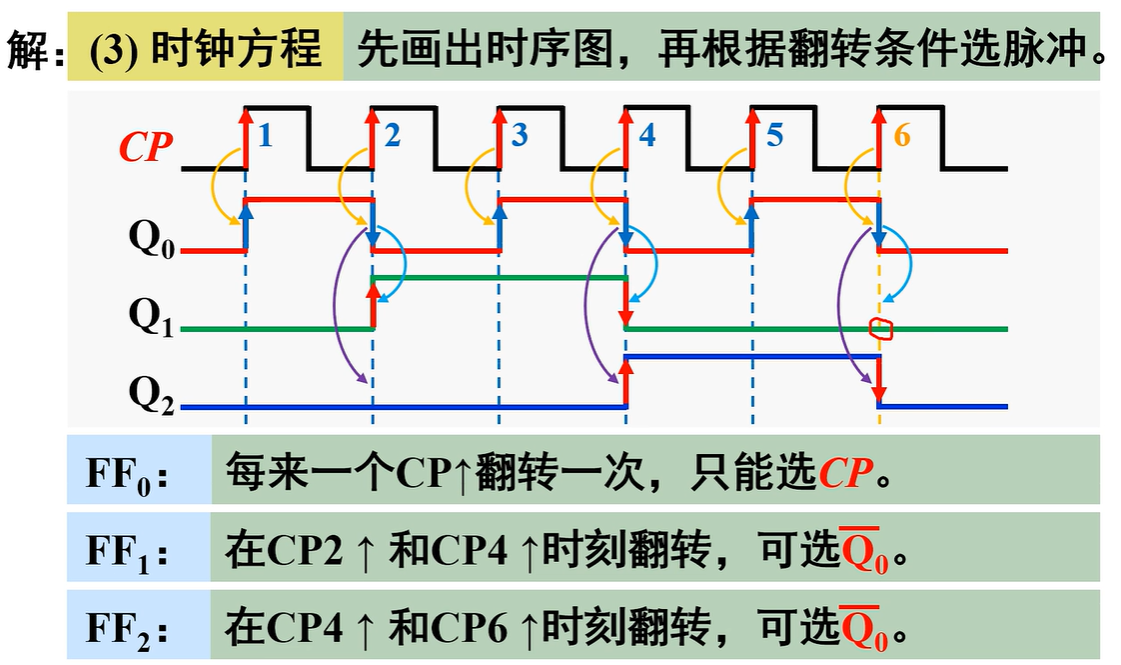
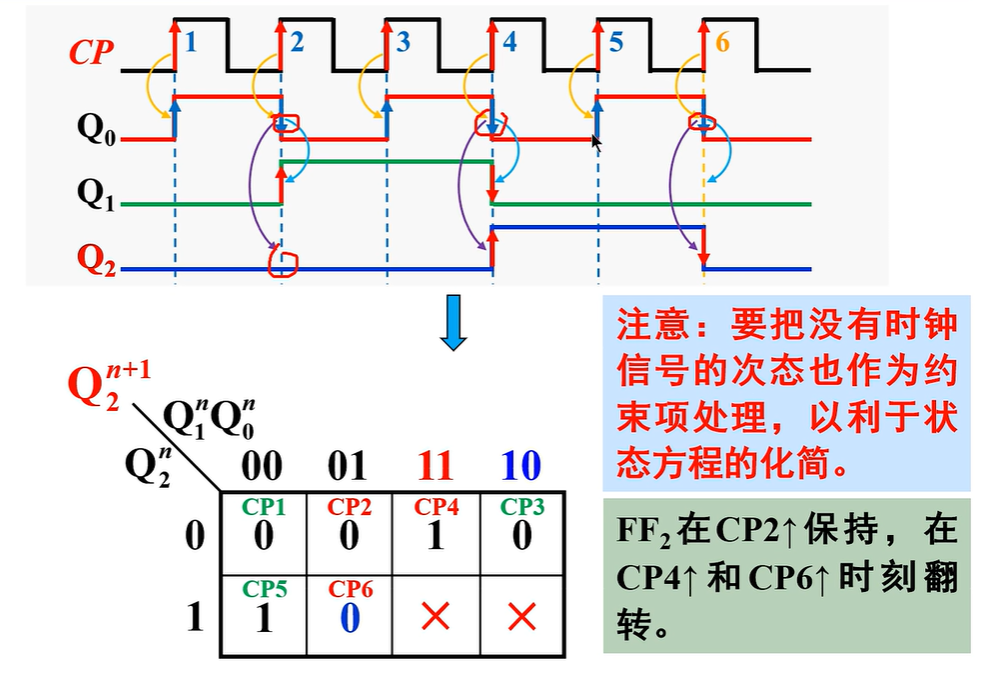
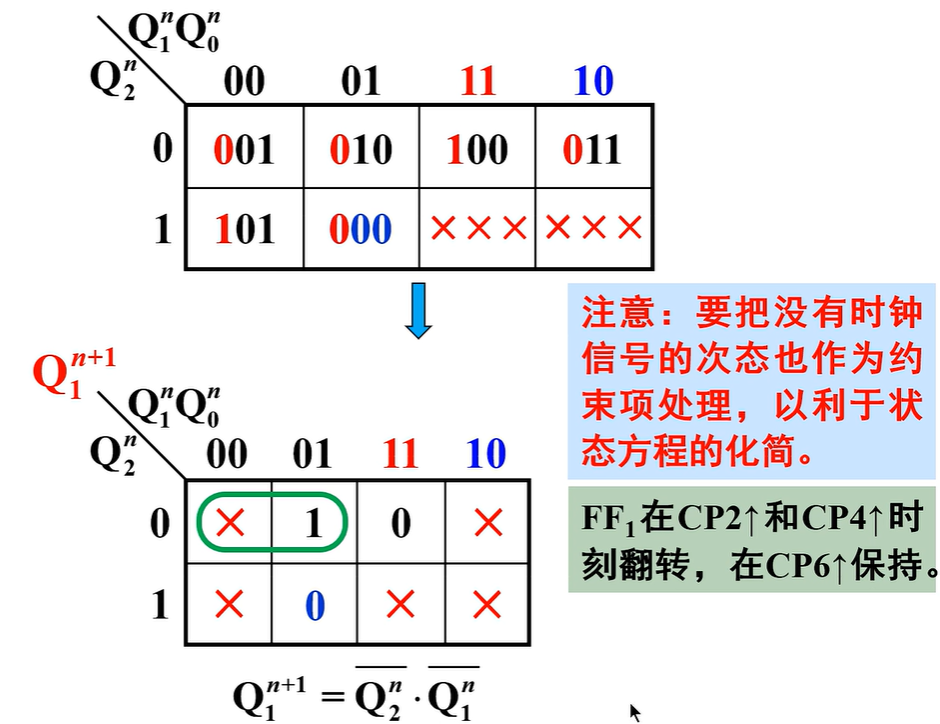
采用异步方案,为了直观清除,需根据状态转换图画出对应的时序图,然后从翻转要求出发,为每个触发器选择合适的时钟信号
选择时钟脉冲的基本原则:凡是要翻转的触发器都能够获得相应的时钟触发沿,且触发沿越少越好
则\(CP_0=CP(CP\uparrow)\)、\(CP_1=CP_2=\bar Q_0(\bar Q_0 \uparrow)\)
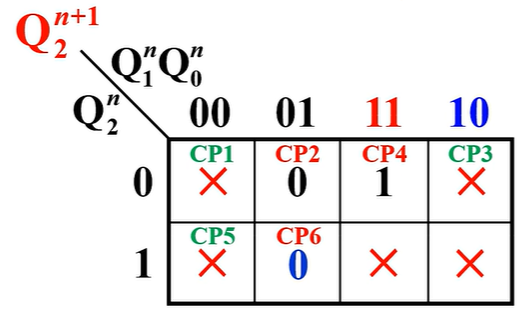
其实意思就是没用到的时钟信号对应的方框中的0或 1 标记为“X”
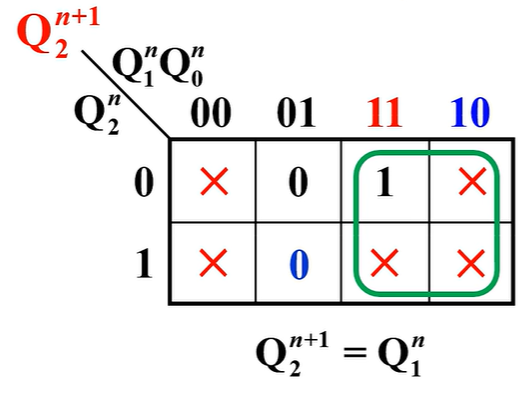
然后再画卡诺圈
因为\(Q_1\)也受\(Q_0\)控制,同样的方式去处理\(Q_1\)
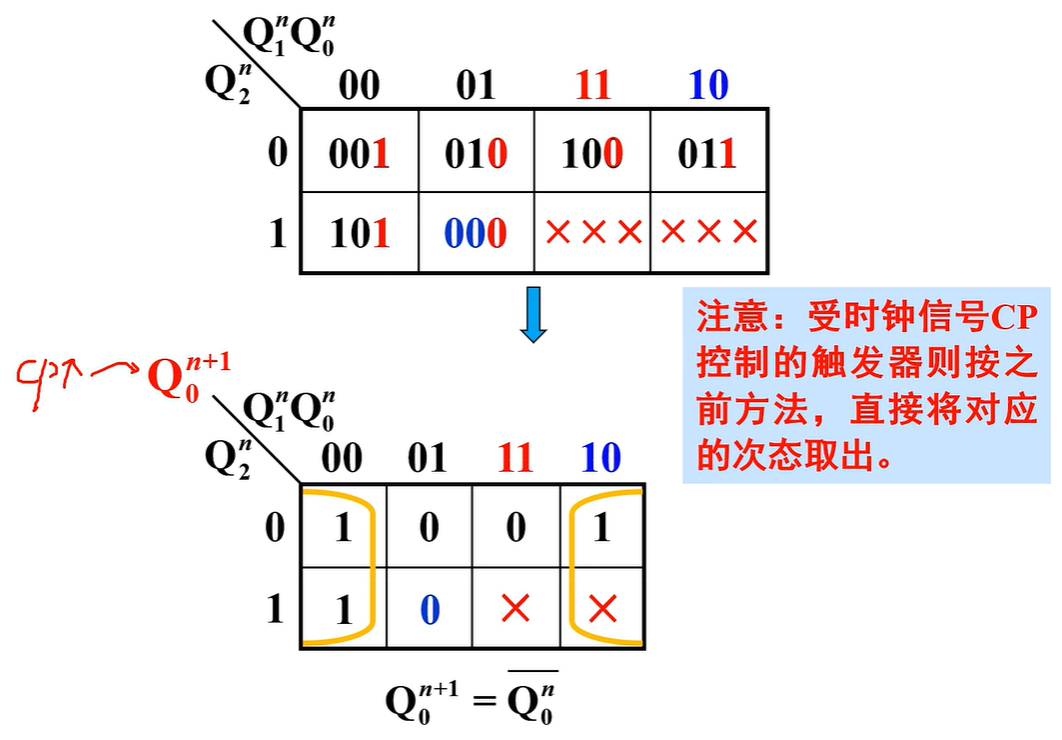
但是\(Q_0\)是受时钟信号CP控制的,所以按之前的方式处理即可