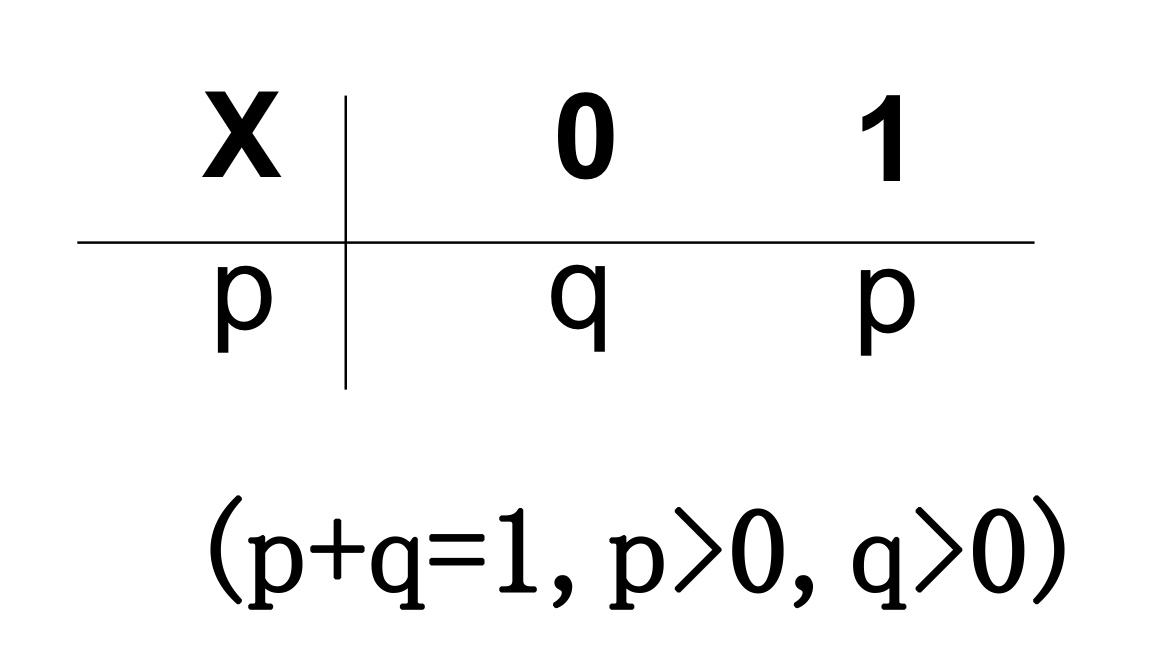Chapter2变量及其概率分布¶

约 1050 个字 8 张图片预计阅读时间 4 分钟

省流

两点分布：$X\sim B(1,p)$ 或者 $X\sim 0-1(p)$
二项分布：$X\sim B(n,p)$
泊松分布：$X\sim P(\lambda)$
超几何分布：$X\sim H(n,a,N)$
帕斯卡分布：$X\sim NB(r,p)$
均匀分布：$X\sim U(a,b)$
指数分布：$X\sim E(\lambda)$
正态分布：$X\sim N(\mu,\sigma^2)$

随机变量是定义在样本空间$S$上的实值单值函数。常用大写字母$X,Y,Z$来表示随机变量，用小写字母$x,y,z$表示其取值

离散型随机变量¶

离散型随机变量(discrete random variable)：

如果随机变量取有限个或可列个值，则此随机变量为离散型随机变量，而若其可能取值为$\{x_i\}$，则称$P\{X=x_k\}=p_k\;,\;k=1,2,...$为$X$的概率分布律(probability mass function)，也可以用列表的方式表达

因为样本空间$S=\{X=x_1,X=x_2,\,...\,,X=x_n\,...\,\}$中各样本点两两不相容，所以：

\[1=P(S)=\sum\limits_{i=1}^{+\infty}P\{X=x_i\}=\sum\limits_{i=1}^{+\infty}{p_i}\]

两点分布¶

如果随机变量$X$的概率分布律为：

\[ P\{X=k\}=p^k(1-p)^{1-k}\;,\;\;\;k=0\;or\;1 \]

则称 $X$ 为服从参数为 $p$ 的 $0-1$ 分布，也称为两点分布，并记为 $X\sim B(1,p)$ 或者 $X\sim 0-1(p)$

二项分布¶

伯努利试验

在 $n$次独立重复试验 中，每次只有 $A$ 和 $\overline A$ 两种结果，且概率不变，则这一系列试验为伯努利试验

注意

如果样本数量足够多，无放回实验可以近似当作有放回实验来处理

若随机变量$X$表示 $n$重伯努利实验中事件A发生的次数，其概率分布律为：

\[ P\{X=k\}={\rm C}_n^kp^k(1-p)^{n-k}\;,\;\;k=0,1,2,...,n \]

注： $1=\left ( p + q \right )^{n} =\sum_{k=0}^{n} C_{n}^{k}p^{k}q^{n-k}$

则称$X$为服从参数为$(n,p)$的二项分布(binomial distribution)，并记为$X\sim B(n,p)$（或$X\sim b(n,p)$）

根据二项式定理，二项分布有如下性质：

\[ \sum\limits_{k=0}^n{\rm C}_n^kp^k(1-p)^{n-k}=1 \]

如果遇到来自于两点分布的总体的，容量为$n$的样本的均值$\overline X$，则有$n·\overline X=\sum\limits_{i=1}^n X_i \sim B(n,p)$

泊松分布¶

如果随机变量$X$的概率分布律为：

\[ P\{X=k\}=\frac{e^{-\lambda}\lambda^k}{k!}\;,\;\;\;k=0,1,2,... \]

其中$\lambda > 0$，则称$X$服从参数为$\lambda$的泊松分布(Poisson distribution)，记做$X \sim P(\lambda)$（或$X \sim \pi(\lambda)$、$X \sim Poi(\lambda)$）

二项分布于泊松分布的近似关系

当$n$足够大，$p$充分小(一般要求$n>10，p<0.1$)，且$np$保持适当大小时，参数为$(n,p)$的二项分布可以用泊松分布近似描述，其中$\lambda = np$，即：

\[ {\rm C}_n^kp^k(1-p)^{n-k} \sim \frac{e^{-\lambda}\lambda^k}{k!}\;\;\;\;\;(n\rightarrow\infty,p<\varepsilon,\lambda=np) \]

事实上：

\[ \begin{gathered} C_n^kp^k\left(1-p\right)^{n-k}=\frac{n!}{k!(n-k)!}\left(\frac\lambda n\right)^k\left(1-\frac\lambda n\right)^{n-k} \\ =\frac{\lambda^k}{k!}\frac{n(n-1)...(n-k+1)}{n^k}\left[\left(1-\frac\lambda n\right)^{-n/\lambda}\right]^{-\lambda}/\left(1-\frac\lambda n\right)^k \\ \approx\frac{e^{-\lambda}\lambda^k}{k!} \\ \end{gathered} \]

因为当n充分大和适当的$\lambda$时

\[ \begin{gathered} \frac{n(n-1)...(n-k+1)}{n^k}\approx1,\left(1-\frac\lambda n\right)^k\approx1,\left[\left(1-\frac\lambda n\right)^{-n/\lambda}\right]^{-\lambda}\approx e^{-\lambda} \end{gathered} \]

超几何分布¶

超几何分布

共有$N$个元素，其中$a$个为$A$类元素，$b$个为$B$类元素，从中任取$n$个元素，$X$为$A$类元素的个数。

如果随机变量$X$的概率分布律为：

\[ P\{X=k\}=\frac{{\rm C}_a^k{\rm C}_b^{n-k}}{{\rm C}_{N}^n}\;,\;\;\;k=l_1,l_1+1,...,l_2 \]

其中$l_1=\max\{0,n-b\}$，$l_2=\min\{n,a\}$，

则称$X$为服从超几何分布(hypergeometric distribution)，并记为$X\sim H(n,a,N)$

几何分布¶

几何分布

事件$A$发生的概率为$p$，则$X$为第一次发生$A$的时候，经历了多少次试验。

如果随机变量$X$的概率分布律为：

\[ P\{X=k\}=p(1-p)^{k-1}\;,\;\;\;k=1,2,... \]

则称$X$为服从参数为 $p$ 的几何分布(geometric distribution)。

$P\left ( X< \infty \right ) =\sum_{n=1}^{\infty}P\left ( X=n \right ) =p\sum_{n=1}^{\infty}\left ( 1-p \right )^{n-1} =\frac{p}{1-\left ( 1-p \right ) } =1 $

帕斯卡分布¶

帕斯卡分布

事件$A$发生的概率为$p$，则$X$为第$r$次发生$A$的时候，经历了多少次试验。

如果随机变量$X$的概率分布律为：

\[ P\{X=k\}={\rm C}_{k-1}^{r-1}p^r(1-p)^{k-r}\;,\;\;\;k=r,r+1,... \]

则称$X$为服从参数为$(r,p)$的帕斯卡分布(Pascal distribution)，也称为负二项分布(negative binomial distribution)，并记为$X\sim NB(r,p)$

分布函数¶

定义：设$X$为随机变量，$x$为任意实数，函数$F(x)=P\{X\leq x\}$为随机变量$X$的概率分布函数，$F$是$\mathbb{R}\to \left [ 0，1 \right ] $的函数，简称为分布函数(distribution function)。

则有以下结论：

\[ P\{x_1<X\leq x_2\}=P\{X\leq x_2\}-P\{X\leq x_1\}=F(x_2)-F(x_1) \]

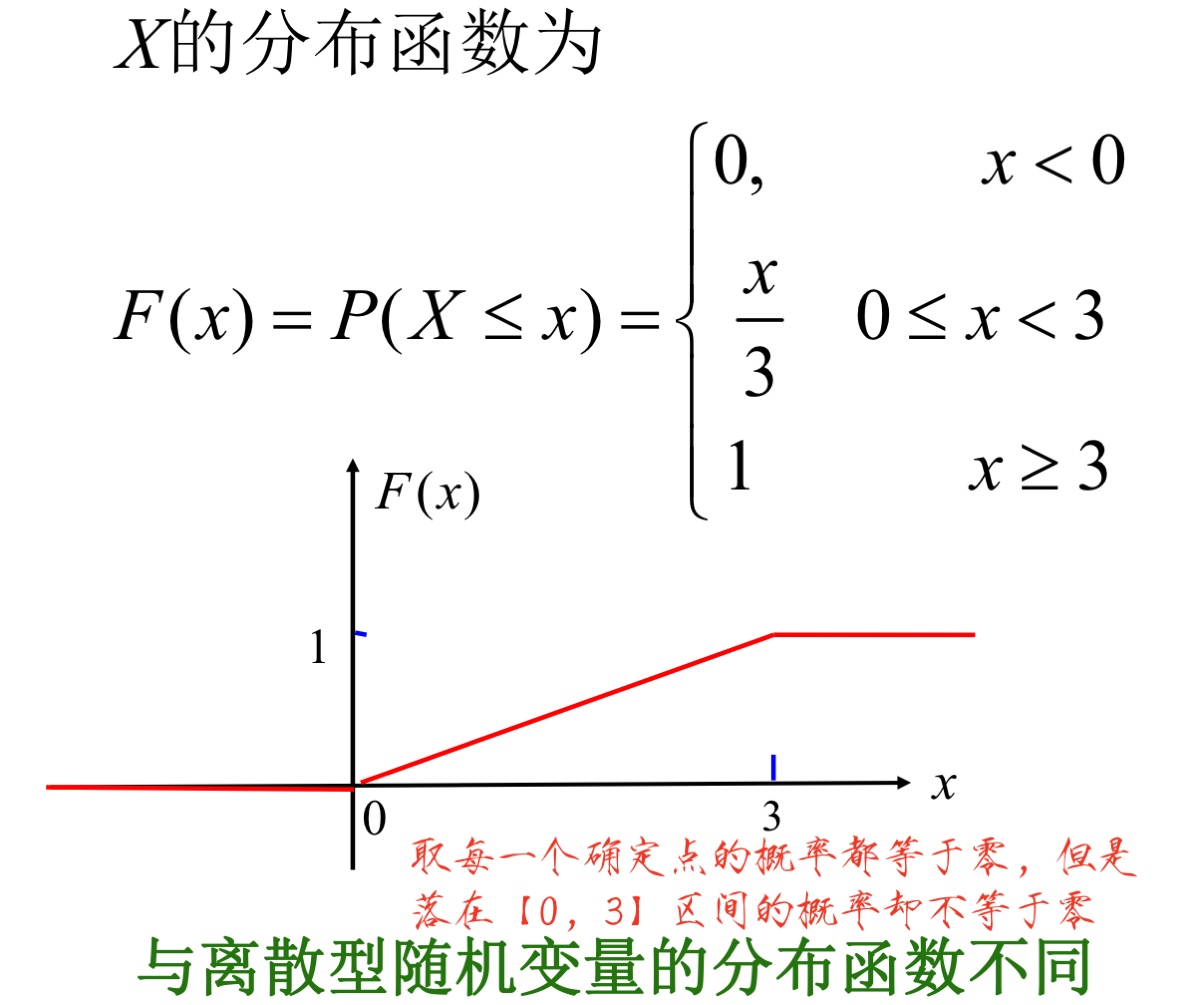
当$X$为离散型随机变量时，设$X$的概率分布律为$P\{X=x_i\}=p_i\;,\;\;i=1,2,...$，则$X$的分布函数为：

\[ F(x) = P\{X\leq x\}=\sum\limits_{x_i\leq x}P\{X=x_i\} \]

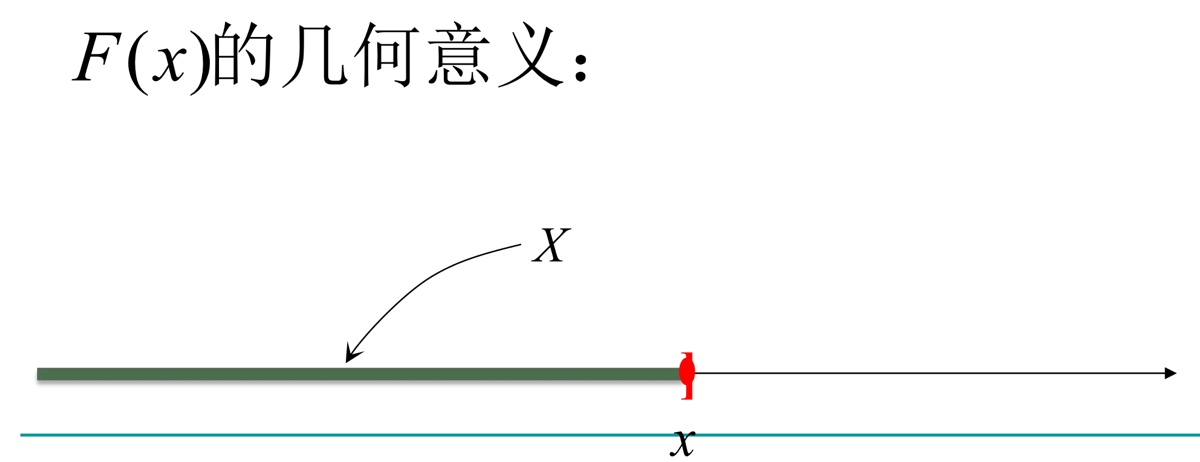
$F(X)$的几何意义

关于$F(x)$有以下结论：

$F(x)$单调不减
$0\leq F(x) \leq 1$且$F(-\infty)=0$，$F(+\infty)=1$
$F(x)$右连续，即$F(x+0)=F(x)=P\{X\leq x\}$
不一定左连续，左极限得到的是 $P\{X<x\}$ ，而不是$P\{X\leq x\}$
$F(x)-F(x-0)=P\{X=x\}$
概率分布函数连续，当且仅当该点的概率等于0
$P\{a<X\leq b\}=F(b)-F(a)$
$P\{X=a\}=F(a)-F(a-0)$($F(a-0)$为分布函数在a点的左极限)
$P\{a\leq X \leq b\}=P\{a<X\leq b\}+P\{X=a\}$

连续型随机变量¶

连续型随机变量与离散型随机变量的不同

密度函数¶

如果对于随机变量$X$，其分布函数为$F(x)$，若存在一个非负的实函数$f(x)$，使对于任意实数$x$，有：

\[ F(x) = \int_{-\infty}^{x}f(t)dt \]

则称$X$为连续型随机变量，并且称$f(x)$为$X$的概率密度函数(probability density function)，简称为密度函数。

关于$f(x)$有以下结论：

$f(x) \geq 0$；
$\int_{-\infty}^{\infty}f(x)dx=1$；
$\forall x_1,x_2\in \mathbf{R}\;\;(x_1<x_2)\;,\;\;P\{x_1<X\leq x_2\}=F(x_2)-F(x_1)=\int^{x_2}_{x_1}f(t)dt$；
在$f(x)$的连续点$x$处，$F'(x)=f(x)$
$P\{X=a\} = 0$，即连续型随机变量任取一个定值的概率为零，因此连续型随机变量落在开区间与相应闭区间上的概率相等；
$P(x<X\leq x+\bigtriangleup x)\approx f(x)\bigtriangleup x$(这表示X落在点x附近$(x，x+\bigtriangleup x]$的概率近似等于$f(x)\bigtriangleup x$)

均匀分布¶

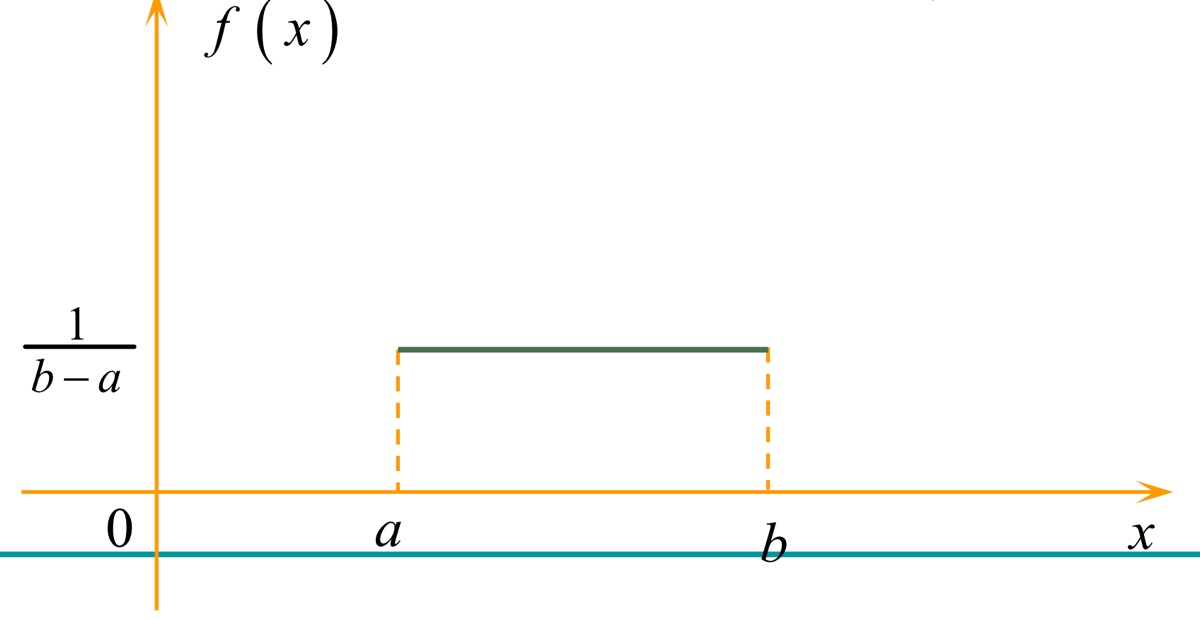
设随机变量$X$就有密度函数：

\[ f(x)=\begin{cases} \frac{1}{b-a}, & x\in(a,b) \\[1ex] 0, & \text{其他} \end{cases} \]

则称$X$服从区间$(a,b)$上的均匀分布，并记为$X\sim U(a,b)$

而得到对应的分布函数为：

\[ F(x)=\begin{cases} 0, & x<a \\[1ex] \frac{x-a}{b-a}, & a\leq x<b \\[1ex] 1, & x\geq b \end{cases} \]

思考题

指数分布¶

若随机变量$X$具有密度函数：

\[ f(x)=\begin{cases} \lambda e^{-\lambda x}, & x>0 \\[1ex] 0，& x\leq0 \end{cases} \]

也有地方写成这样：

\[ f(x)=\begin{cases} \frac{1}{\theta} e^{-\frac{1}{\theta} x}, & x>0 \\[1ex] 0，& x\leq0 \end{cases} \]

其中$\lambda > 0$，则称$X$服从参数为$\lambda$的指数分布(exponential distribution)，记为$X\sim E(\lambda)$

指数分布对应的分布函数为：

\[ F(x)=\int_{-\infty}^{x}f(t)\mathrm{d}t= \begin{cases} 1-e^{-\lambda x}, & x>0 \\[1ex] 0，& x\leq0 \end{cases} \]

指数分布具有无记忆性，即$P(X>t_0+t | X>t_0)=P(X>t)$。

指数分布的无记忆性

假设 $t_0>0$，$t>0$，

\[ \begin{aligned} P(X>t_0+t \;\; | \;\; X>t_0 ) & = \frac{P(X>t_0+t)}{P(X>t_0)} \cr & = \frac{1-F(t_0+t)}{1-F(t_0)} \cr & = e^{-\lambda t} = P(X>t) \end{aligned} \]

\[ \begin{aligned} P(X\lt t_0+t \;\; | \;\; X>t_0) & = \frac{P(t_0\lt X\lt t_0+t)}{P(X>t_0)} \cr & = \frac{F(t_0+t)-F(t_0)}{1-F(t_0)} \cr & = 1-e^{-\lambda t} = P(X<t) \end{aligned} \]

无记忆性的一个例子

假设设备无故障运行的时间 $T$ 服从指数分布。已知设备无故障运行了10个小时，求该设备再无故障至少运行8个小时的概率。

\[ P\lbrace T\geq 18 \; | \; T>10 \rbrace = \frac{P\lbrace T>18\rbrace }{P\lbrace T>10\rbrace} = e^{-8\lambda} = P\lbrace T>8\rbrace \]

注意到，这一条件概率与无条件下无故障运行8小时的概率没有区别。

正态分布¶

如果随机变量$X$具有密度函数：

\[ f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\;, \;\;\; |x|<+\infty \]

其中$\sigma>0\;,\;|\mu|<+\infty$为常数，则称$X$服从参数为$(\mu,\sigma)$的正态分布(normal distribution / Gauss distribution)，或者称$X$为正态变量，记为$X\sim N(\mu,\sigma^2)$。

其对应的分布函数为：

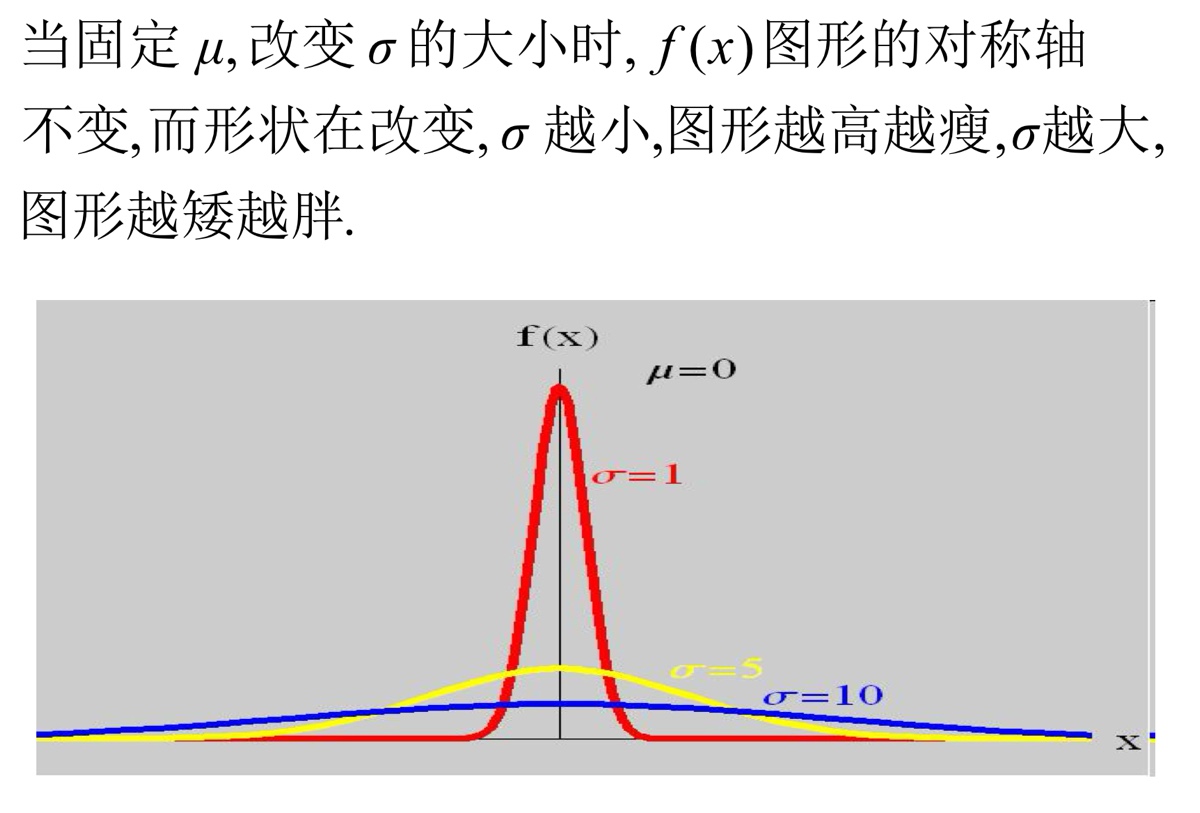
\[ F(x)=\int_{-\infty}^{x}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(t-\mu)^2}{2\sigma^2}}dt \]

在上面出现的式子中，$\mu$为位置参数，决定了分布图像的对称轴位置；$\sigma$为尺度参数，决定了形状，$\sigma$越小，图像越集中。