Chapter 1 概率论的基本概念¶

约 1322 个字 2 张图片预计阅读时间 4 分钟

样本空间与随机事件¶

随机试验(random experiment) 的特点：¶

可以在相同条件下重复进行；
事先知道所有可能的结果；
进行实验时并不知道哪个结果会发生

而随机试验的所有可能结果构成的集合为样本空间(sample space)，记为\(S\)

其中的每一个元素\(e\)为样本点(sample point)。
而样本空间的任一子集\(A\)成为随机事件(random event)，简称事件。

特别的

只含有一个样本的子集称为基本事件。
每次事件\(S\)总是发生，称为必然事件

事件的相互关系¶

两互逆事件又称对立事件。
若\(AB=\varnothing\)，则称两事件不相容（或互斥）
若\(A\subset B \;and\;B\subset A\)，则称两事件相等

其中，和、交、逆事件有如下运算规律：

交换律：\(A\cup B=B\cup A\;,\;A\cap B=B\cap A\)；
结合律：\(A\cup(B\cup C)=(A\cup B)\cup C\;,\;A(BC)=(AB)C\)；
分配律：\(A(B\cup C)=(AB)\cup(AC)\;,\;(AB)\cup C=(A\cup C)(B\cup C)\)；
对偶律 / 德摩根定律(De Morgan's law)：\(\overline{\bigcup\limits^n_{j=1}A_j}=\bigcap\limits^n_{j=1}\overline{A_j}=\overline{A_1}\cup\overline{A_2}\cup…\overline{A_n}\;,\;\overline{\bigcap\limits^n_{j=1}A_j}=\bigcup\limits^n_{j=1}\overline{A_j}=\overline{A_1}\overline{A_2}…\overline{A_n}\)；

串联系统与并联系统：¶

串联系统：\(A=\bigcap\limits_{i=1}^nA_i\)
并联系统：\(A=\bigcup\limits_{i=1}^nA_i\)

频率与概率¶

频率 = 频数 / 试验总次数

定义：记\(f_n(A)=\frac{n_A}{n}\) * \(n_A\)：A发生的次数（频数） * \(n\)：总试验次数 * \(f_n(A)\)为事件A的频率

若样本空间\(S\)中的任一事件\(A\)，定义概率\(P(A)\)满足以下三条公理：

非负性\(P(A)\geq0\)；
规范性 / 正则性\(P(S)=1\)；
可列可加性：对于\(S\)中不相容的事件\(A_i\)，有\(P(\bigcup\limits^{+\infty}_{j=1}A_j)=\sum\limits_{j=1}^{+\infty}P(A_j)\)；

由此得到如下几条概率的性质：

对于有限个两两不相容的事件的和事件，有 \(P(\bigcup\limits^n_{j=1}A_j)=\sum\limits_{j=1}^nP(A_j)\)；
\(P(A)=1-P(\overline A)\)；特别的，可以得到\(P(\varnothing)=0\)；
当\(A\supset B\)时，\(P(A-B) = P(A)-P(B)\)且\(P(A)\geq P(B)\)；
概率的加法公式：\(P(A\cup B)=P(A)+P(B)-P(AB)\)；推广即容斥原理；
加法公式的推论：\(P(A\cup B)\leq P(A)+P(B)\)；

等可能概型¶

如果随机事件满足：

\(S\)中样本点数有限；
\(\forall i,j \in\{1,2,...,n\},\;P(e_i) = P(e_j)\)，即等可能；

则该试验问题为等可能概型（古典概型）
有如下性质：若总事件个数为 \(N\)，\(A\) 为 \(n\) 个基本事件的和事件，则 \(P(A)=\frac{n}{N}\)。

条件概率¶

如果\(P(B)>0\)，那么定义在\(B\)发生的条件下\(A\)发生的条件概率(contidional probability)为：
\(P(A|B)=\frac{P(AB)}{P(B)}\)

条件概率是在新的样本空间下的概率度量，它满足概率的定义和性质。

定义完备事件组为\(S\)的一个划分\(B_1,B_2,...,B_n\)，它满足如下性质：

不重：\(B_iB_j=\varnothing,i,j,...,n,i\not=j\)；
不漏：\(\bigcup\limits^n_{i=1}B_i=S\)；

设\(S\)为一样本空间，\(A\)为该试验的事件，\(\{B_i\}\)为\(S\)的一个划分，则有：

若\(A_1,...,A_n,...\)互不相容，则\(P(\bigcup\limits_{n=1}^{\infty}A_n|B)=\sum\limits_{n=1}^{\infty}P(A_n|B)\)；
乘法公式：当\(P(A)\not=0\;\,\;P(B)\not=0\)时，有\(P(AB)=P(A)*P(B|A)=P(B)*P(A|B)\)；
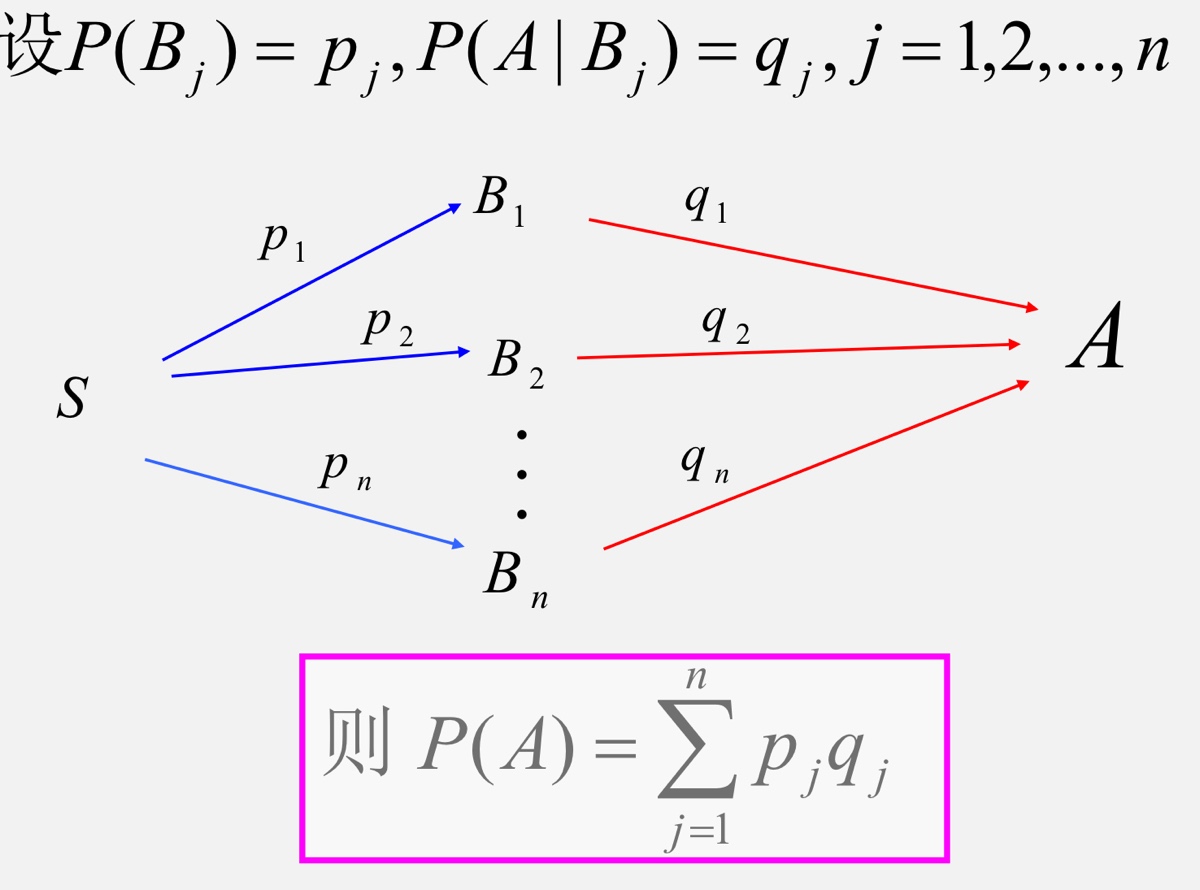
全概率公式：\(P(A)=\sum\limits_{j=1}^nP(B_j)P(A|B_j)\)；

路径图：画出路径图求解问题

贝叶斯公式：\(P(B_k|A)=\frac{P(B_kA)}{P(A)}=\frac{P(B_k)P(A|B_k)}{\sum\limits_{j=1}^nP(B_j)P(A|B_j)}=\frac{p_iq_i}{\sum\limits_{j=1}^n p_jq_j}\)；
- 其中，我们称\(P(B_j)\)这种事先知道的概率为先验概率；
- 而\(P(B_j|A)\)这种，当事件\(A\)发生后需要修正 \(B_j\) 的概率成为后验概率（知道了额外的信息：A发生）。
- 我们称\(P(A|B_j)\)为似然概率。

事件独立性与独立试验¶

独立的定义：设\(A,B\)为两个随机事件，若有\(P(AB)=P(A)*P(B)\)，则\(A,B\)相互独立(independent)

其实际意义是，事件\(A\)的发生与事件\(B\)的发生互不影响。
那么就有结论： \(P(AB)=P(A)*P(B)\Longleftrightarrow P(A|B)=P(A)\)；

\(A,B\)相互独立\(\Longleftrightarrow\) \(A,\overline{B}\)相互独立\(\Longleftrightarrow\) \(\overline{A},B\)相互独立\(\Longleftrightarrow\) \(\overline{A},\overline{B}\)相互独立

当出现两个以上的随机事件时，如三个随机事件\(A,B,C\)，当： \(P(AB)=P(A)*P(B)\;,\;P(AC)=P(A)*P(C)\;,\;P(BC)=P(B)*P(C)\) 都成立，则称事件\(A,B,C\)两两独立；

如果同时还满足：
\(P(ABC)=P(A)P(B)P(C)\) 则称事件\(A,B,C\)相互独立。

显然有：相互独立 \(\Rightarrow\) 两两独立(相互独立比两两独立来的更强)
两两独立不能 \(\Rightarrow\) 相互独立

例：

更普遍的：
定义\(\{A_i\}\)相互独立当且仅当\(\forall{i_j},\;P(\prod\limits_{j=1}^k A_{i_j})=\prod\limits_{j=1}^kP(A_{i_j})\)

独立试验与重复试验：

独立试验各个试验结果互不影响；
重复试验的每一次子试验都在相同情况下进行；