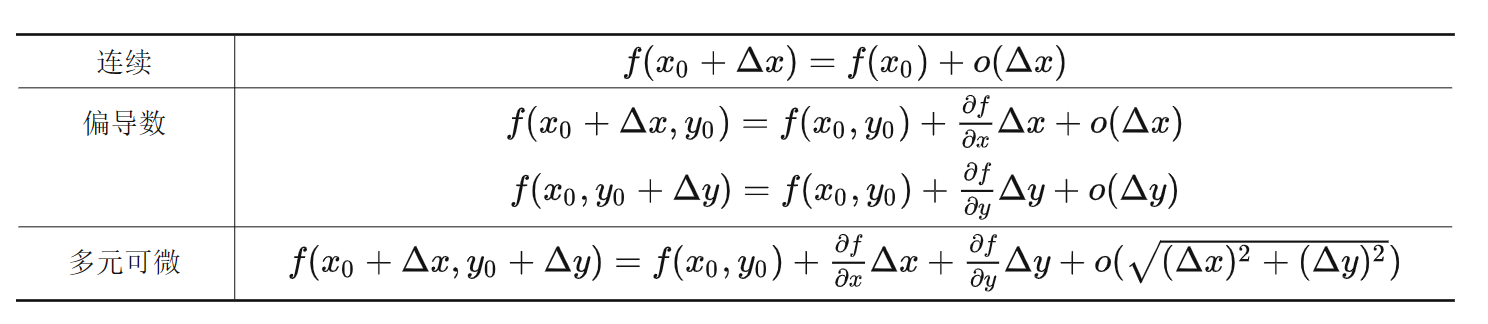Chapter 2 解析函数¶

约 1132 个字 9 张图片预计阅读时间 4 分钟

复变函数¶

$w=f(z)=f(x+iy)=u(x,y)+iv(x,y)$

极限¶

$\lim\limits_{z\rightarrow z_0}f(z)=A\ \Leftrightarrow$ $\lim\limits_{x\rightarrow x_0,y\rightarrow y_0}u(x,y)=u_0,\lim\limits_{x\rightarrow x_0,y\rightarrow y_0}v(x,y)=v_0$

连续¶

$\lim\limits_{z\rightarrow z_0}f(z)=f(z_0) \Leftrightarrow \forall \epsilon > 0 ~\exists~δ(ε)>0$，当$0<|z-z_0|<δ时，|f(z)-f(z_0)|<ε$

$\Leftrightarrow $ 对应的实函数u,v分别连续（左极限=右极限=$f(z_0)$）

在闭区域$\overline G$中连续的函数有两个重要性质

$|f(z)|$在$\overline G$中有界，并达到它的上下界
$f(z)$在$\overline G$中一致连续，即对于任意 ε>0，存在与z无关的$δ(ε)>0$，在$\overline G$中的任何两点$z_1,z_2$,只要满足$|z_1-z_2|<δ$,就有$|f(z_1)-f(z_2)|<ε$

若两函数在$z_0$连续，则其$+,-\times,\div$(分母$\ne 0)$复合运算后，在点$z_0$仍连续

求导¶

$f'(z_0)=\lim\limits_{\Delta z\rightarrow 0}\frac{f(z_0+\Delta z)-f(z_0)}{\Delta z}$

导数的可视化

可导的定义是：函数f(z)在 $z=z_0$ 这一点可导，则 $f'(z_0)=\lim_{\Delta z\to0}\frac{f(z_0+\Delta z)-f(z_0)}{\Delta z}$ 存在

导数如何进行可视化呢？我们画一个例子来看看：

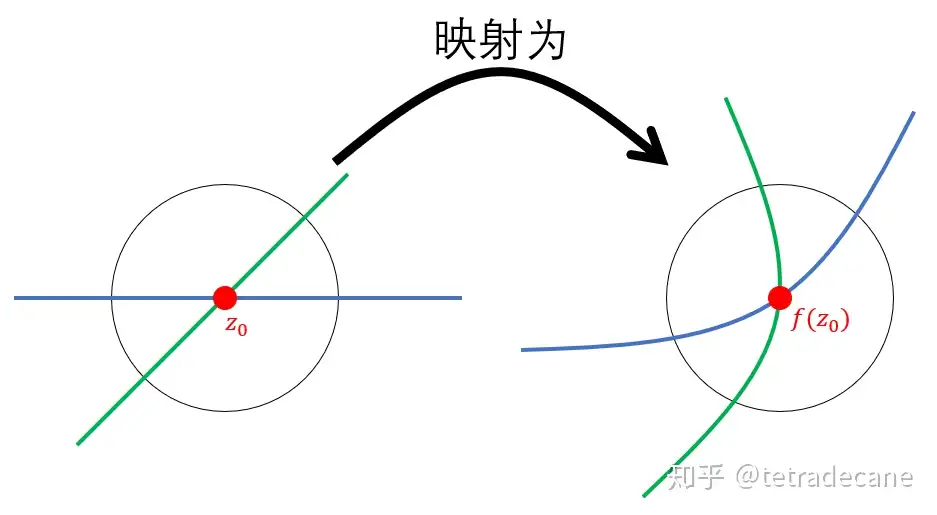
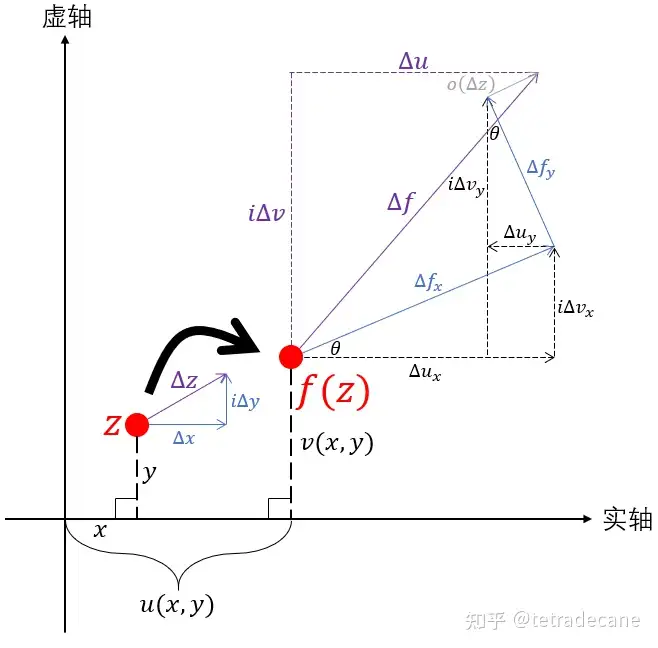
如图所示，我们观察f(z)的一个点 $z=z_0$ 及其映射之后的状况。蓝线和绿线分别是通过该点 $z_0$ 的直线，经过映射之后可能会变成曲线

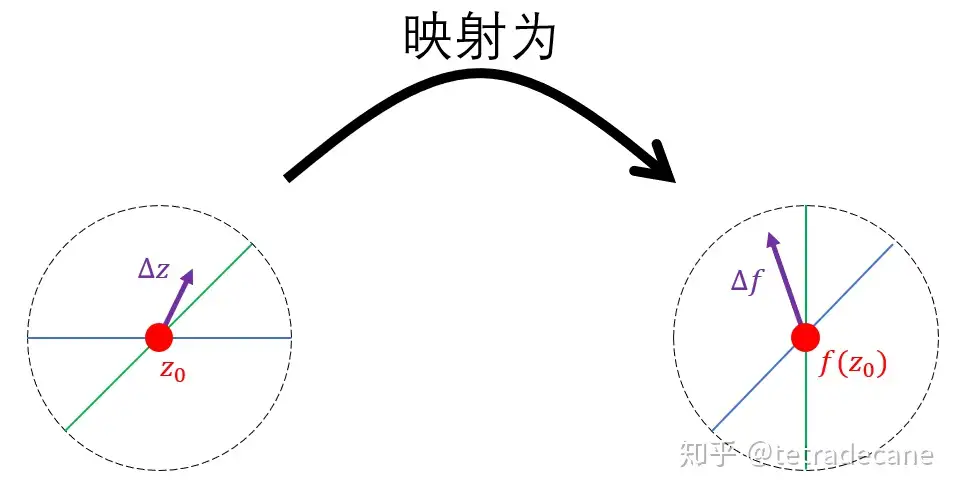
让这个邻域足够小，则经过这一点的光滑曲线可以近似为直线。自变量的微分 $\Delta z$就是从点 $z_0$ 往任意方向走一个微小距离对应的复数，相应地，应变量的微分 $\Delta f=f(z_0+\Delta z)-f(z_0)$ 是从点 $f(z_0)$ 往相应方向走一个相应距离对应的复数，如图所示：

f(z)在 $z_0$ 可导，即 $f'(z_0)=\lim_{\Delta z\to0}\frac{\Delta f}{\Delta z}$ 存在。根据极限的唯一性，我们知道 $\Delta z$ 不论往任何方向走， $f'(z_0)$ 的值都是唯一的

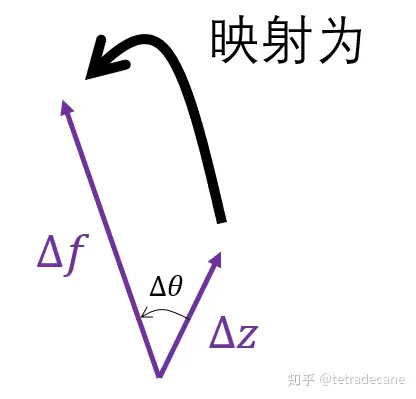
复数的除法有运算法则 $\frac{z_2}{z_1}=\frac{r_2}{r_1}\angle(\theta_2-\theta_1)$ ，即模长相除，辐角相减。因此

$\frac{\Delta f}{\Delta z}=\frac{|\Delta f|}{|\Delta z|}\angle(\mathrm{Arg}\Delta f-\mathrm{Arg}\Delta z)$

如果 $f'(z_0)\neq0$ ，则 $\mathrm{Arg}f'(z_0)=\lim_{\Delta z\to0}(\mathrm{Arg}\Delta f-\mathrm{Arg}\Delta z)$和 $|f'(z_0)|=\lim_{\Delta z\to0}\frac{|\Delta f|}{|\Delta z|}$ 都是定值，我们称这两个量分别为转动角和伸缩率，如下图所示：

也就是说，如果一个函数f(z)在z处可导且导数不为0，那么z附近的微小邻域在经过映射f之后，大约会整体旋转 $\mathrm{Arg}f'(z_0)$ 的角度，并放缩为原来的 $|f'(z_0)|$ 倍。这就是复变函数导数的几何意义

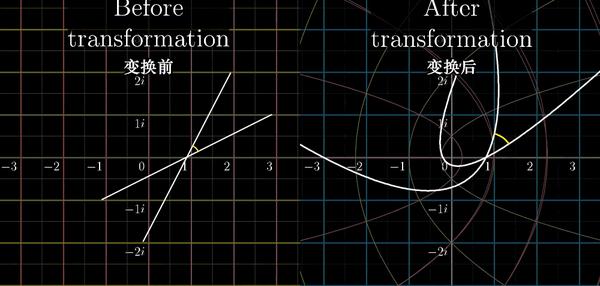
根据上述结论，如果函数f(z)在某个区域解析，则这个区域中的任意两条直线（例如图2中的蓝线和绿线）在经过映射f之后会保持夹角不变（除导数为0的情况），我们称此时f(z)具有保角性。保角性加伸缩率不变性称为保形性。因此，复变函数在某个区域解析，则可推出其在这个区域具有保形性

如图是个展现函数 $f(z)=z^2$ 具有保角性的直观的动图：

复变函数的实部函数与虚部函数

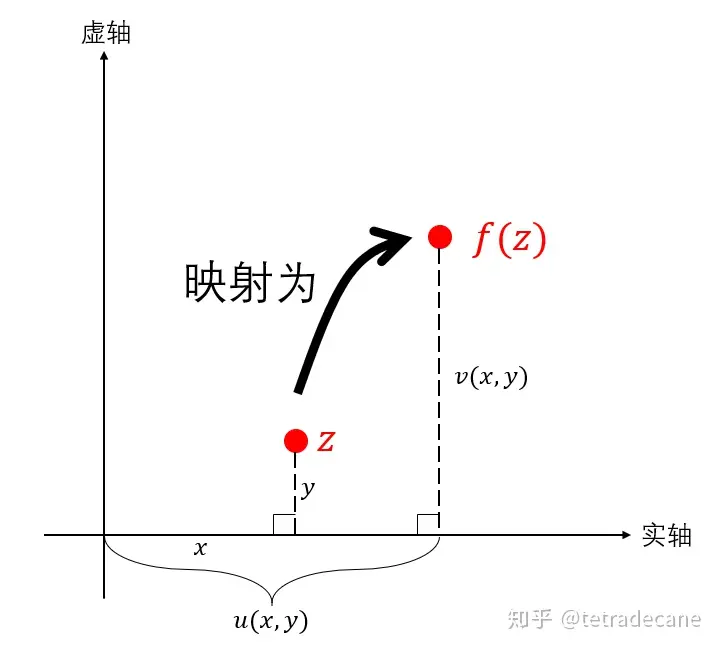
复变函数不仅可以记为f(z). 因为自变量和应变量都是复数，我们可以用复数的坐标形式（即x+yi这种形式）来表示它们，并研究它们的性质

我们记自变量z=x+yi，函数值f(z)=u+vi，其中x, y, u, v均是实数。用x与y的值可以决定z的值，继而决定f(z)的值，继而决定u与v的值，因此在确定复变函数f(z)的情况下，u和v都是关于x和y的实二元函数，那么f(z)就可以记为f(z)=u(x, y)+v(x, y)i. 我们称u(x, y)和v(x, y)分别是f(z)的实部函数和虚部函数

如图是实部函数与虚部函数的几何意义：

如果f(z)可导，二元函数u和v会有什么性质呢？

可微性

如图所示，自变量z有增量 $\Delta z=\Delta x+i\Delta y$，应变量f也有相应的增量 $\Delta f$ . 如果f'(z)存在，有

$\begin{align} \Delta f&=f'(z)\Delta z+o(\Delta z)\\ &=\Delta f_x+\Delta f_y+o(\Delta z)\\ &=\Delta u_x+i\Delta v_x+\Delta u_y+i\Delta v_y+o(\Delta z)\\ &=\Delta u+i\Delta v\\ \end{align}$

其中 $\Delta f_x$ 是由 $\Delta x$ 带来的增量， $\Delta f_y$ 是由 $\Delta y$ 带来的增量

记 $f'(z)=k\angle\theta$ ，即k为伸缩率， $\theta$ 为转动角，根据保形性，可得

$\Delta f_x=\Delta x\times k\angle\theta=k\Delta x\angle\theta=\Delta x f'(z)$

$\Delta f_y=i\Delta y\times k\angle \theta=k\Delta y\angle\left(\theta+\frac\pi2\right)=i\Delta yf'(z)$

记 $\rho=|\Delta z|=\sqrt{(\Delta x)^2+(\Delta y)^2}$ ，可得

\[ \begin{align} \Delta u&=\Delta u_x+\Delta u_y+\Re o(\Delta z)\\ &=\Re(\Delta f_x+\Delta f_y+o(\Delta z))\\ &=k\Delta x\cos\theta-k\Delta y\sin\theta+o(\rho)\\ &=\Delta x\Re f'(z)-\Delta y\Im f'(z)+o(\rho)\\ \end{align}\tag{1} \]

\[ \begin{align} \Delta v&=\Delta v_x+\Delta v_y+\Im o(\Delta z)\\ &=\Im(\Delta f_x+\Delta f_y+o(\Delta z))\\ &=k\Delta x\sin\theta+k\Delta y\cos\theta+o(\rho)\\ &=\Delta x\Im f'(z)+\Delta y\Re f'(z)+o(\rho)\\ \end{align}\tag{2} \]

其中符号 $\Re$ 表示取实部（相当于Re），符号 $\Im$ 表示取虚部（相当于Im）

因此，根据二元函数可微的定义，u和v都具有可微性

微积分回忆内容¶

连续、可导和可微¶

偏导数存在且偏导数连续，一定可微
可微一定可导，可导不一定可微
一般看不可导：沿着两条不同方向线趋近某点，不一样推出矛盾

解析性¶

定义

$f(z)$在$z_0$的某个邻域内的每一点可导 $\Leftrightarrow$ $f(z)$在$z_0$点解析/正则
$f(z)$在区域D内的每一点可导 $\Leftrightarrow$ $f(z)$在区域D内解析/正则
$\Leftrightarrow$ $f(z)$在D内的任意点$z_0$（存在$z_0$的一个邻域）处均可展开为收敛的幂级数
奇点：不解析的点
孤立奇点：$D(z_0,\delta)$内的唯一奇点

判别法¶

同时满足

$u(x,y),v(x,y)$在$(x,y)$点的邻域内（或D内）可微
Cauchy-Riemann条件（C-R条件）

C-R条件¶

\[ \Large \left \{ \begin{array}{} \frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}\\ \frac{\partial u }{\partial y}=-\frac{\partial v}{\partial x} \end{array} \right. \]

柯西-黎曼方程

根据二元函数微分的性质，可得

$\Re f'(z)=\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y},~\Im f'(z)=\frac{\partial v}{\partial x}=-\frac{\partial u}{\partial y}$

于是我们称 $\begin{cases} \frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}\\ \frac{\partial v}{\partial x}=-\frac{\partial u}{\partial y}\\ \end{cases}$ 为柯西-黎曼方程（Cauchy-Riemann Equations），简称为C-R方程

实际上，可以证明：两个可微二元实函数u(x, y)和v(x, y)构成的复变函数f=u+vi在区域D内解析的充要条件是u和v在D内满足C-R方程

C-R方程可以更轻松地导出，便于记忆

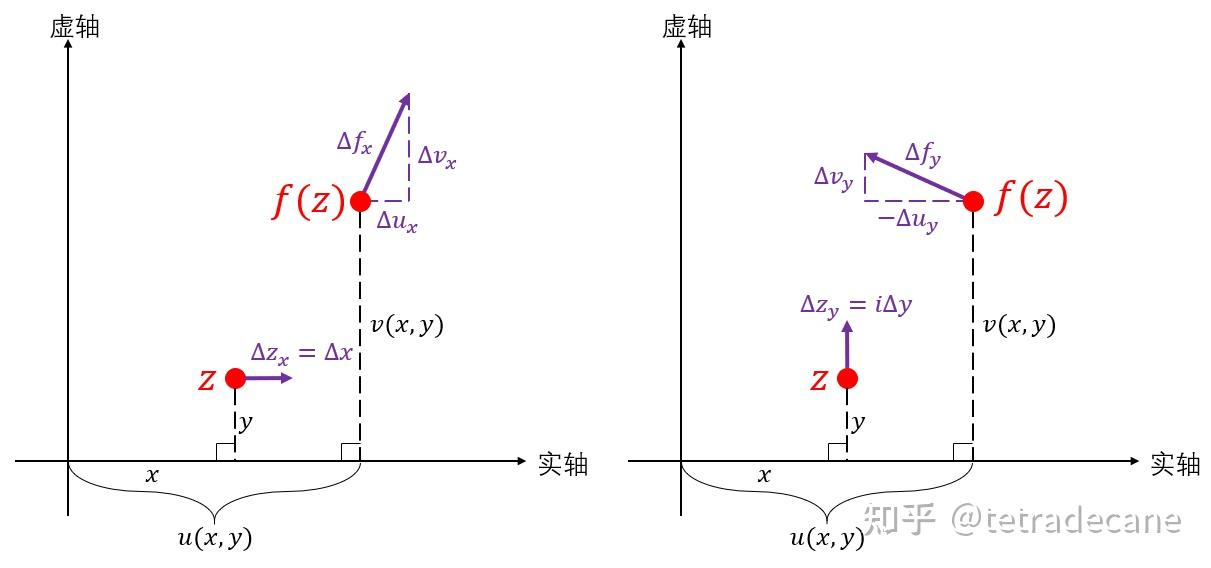
如图所示，指定 $\Delta z$ 为沿着x轴（图8左）和沿着y轴（图8右）的两个特殊方向。当 $\Delta x=\Delta y$ 时，根据保形性，两个紫色直角三角形近似全等，于是

$\Delta u_x\approx\Delta v_y,~\frac{\Delta u_x}{\Delta x}\approx\frac{\Delta v_y}{\Delta y}$

取 $\Delta x=\Delta y\to0$ 的极限即可得到 $\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}$ . 同理可得 $\frac{\partial v}{\partial x}=-\frac{\partial u}{\partial y}$

注意，本例中 $\Delta u_y$ 是负的，故计算三角形边长的时候要加个负号。当 $\Delta f$ 取其他方向的时候可以类似讨论

为什么C-R方程里面有个负号？为什么函数u和v不是对称的？

直观上来说，C-R方程的基础是复变函数的保形性，其中包括旋转不变性。而旋转对称本身就不是关于x和y坐标对称的。旋转在复数中可用乘法来表示，任何一个复数乘以实数单位元1会停留在原处，而乘以虚数单位元i则会绕原点正向旋转 $90^\circ$ ，这就是旋转关于坐标轴的不对称性的一个体现

对于解析的复变函数而言，u是实部函数，而v是虚部函数，因为x和y坐标旋转不对称，它们自然也不对称

相对地，关于x和y坐标对称的变换，是关于直线y=x轴对称的这种形式

注意

如果满足条件的是孤立的点，那么只能说$f(z)$在该点上可导，而不解析
解析函数的复合函数（加、减、乘、除等解析函数）仍为解析函数
反函数解析法则：设$w=f(z)$在区域D内单叶解析，$(f^{-1}(w))^{\prime}=\frac{1}{f^{\prime}(z)}=\frac{1}{f^{\prime}[f^{-1}(w)]}$

单叶函数：在区域D上解析的单值复变函数$f(z)$，若对D中任意不同的两点$z_1,z_2$，有： $f(z_1)\neq f(z_2)$，则说f(z)为D上的单叶函数
$f(z)=\bar{z}$ 处处不可微，处处不解析

解析函数 $f(z)$ 退化为常数的充分条件

若$f(z)$在D上解析，且满足以下条件之一：
1. 导数恒为0
2. 解析函数的实部、虚部、幅角、模中有1恒为常数
3. $\overline{f(z)}$ 在D上解析则$f(z)$在D内恒为常数
另若$f(z)$在整个复平面解析，见柳维尔定理解析性

小结

函数 f(x) 在区域D解析的等价条件有：

函数 f(x) 在区域 D内可导
Re(f),Im(f)在区域D内可微且满足Cauchy-Riemann条件
函数 f(x) 在区域 D内连续且积分与路径无关
函数 f(x) 在区域 D内可展开为幂级数

调和函数¶

定义¶

如果实函数 $U\left ( x,y \right ) $ 在区域$D$内有二阶连续偏导数并满足拉普拉斯方程 $\Delta U=\frac{\partial^{2} U}{\partial x^{2} }+ \frac{\partial^{2} U}{\partial y^{2} }=0,inD$ ,则称 $U\left (x,y \right )$ 为D内的调和函数

定理¶

$f(z)=u(x,y)+iv(x,y)$ 是区域 $D$ 内的解析函数则 $u(x,y),v(x,y)$ 在 $D$ 内均为调和函数

常见初等函数¶

全部初等函数（多项式函数、指数函数、三角函数、对数函数、幂函数……）在相应的定义域上都是解析的

指数函数¶

$\Large w=e^z=e^{x+iy}=e^x(\cos y+i\sin y)$

求导等同实指数函数:

$\left ( e^{z} \right )^{\prime}=e^{z}$ （$dz = d(x+iy$））

在整个复平面上处处解析

$e^{z} $为指数函数，则

$e^{z+w}=e^{z}\cdot e^{w}$对所有 $z,w\in \mathfrak{C} $ 成立，所以 $\left ( e^{z} \right ) ^{n} =e^{zn} $
$e^{z}\ne 0$如果z=x为实数，当$x> 0，e^{z}>1 ,x< 0，e^{z}<1 $
$e^{z}$是周期函数，其周期$T = 2n\pi i$(n为整数，$n \ne 0$)
$e^{\frac{\pi}{2}i} =i,e^{\pi i} =-1,e^{\frac{3\pi}{2}i} =-i,e^{2\pi i} =1$
$e^{z}=1$的充分必要条件是$z = 2n\pi i$(n为整数)

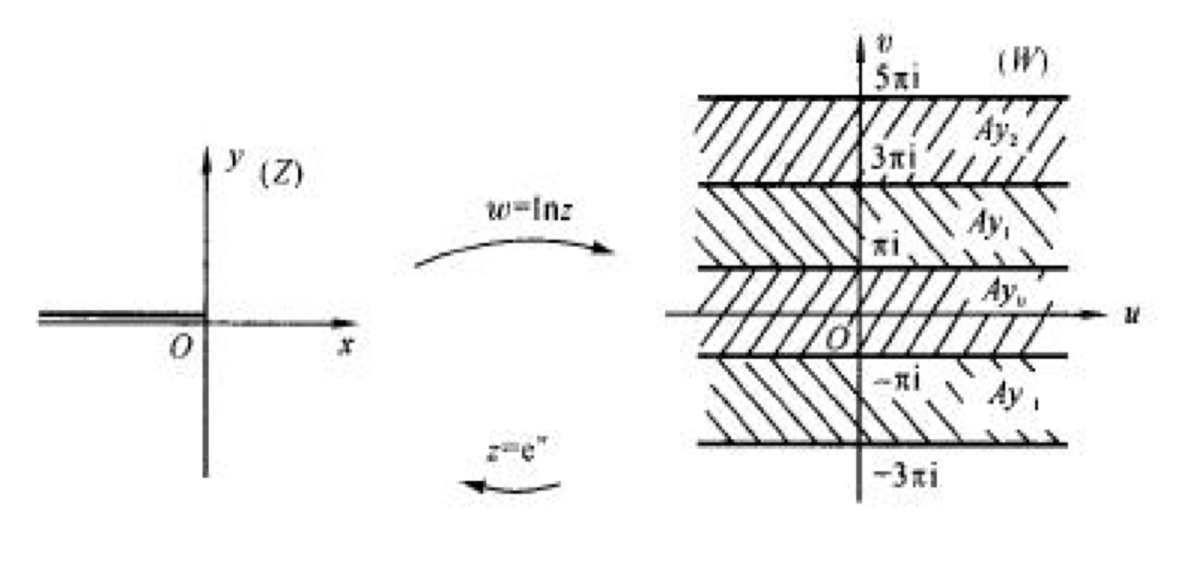
对数函数¶

$\Large w=Ln z=lnz+i2k\pi=ln|z| + i Arg z=(ln|z|+iargz) +2ki\pi$

$\Large =ln|z|+i(argz +2k\pi)$

对数函数 $Ln z$ 是多值函数，有无穷多个分支，k=0时的分支称为对数函数的主支，记： $Lnz=ln|z|+iargz$ 为对数函数主支

显然，$Lnz=lnz+i2k\pi$

基本性质

$Ln(z_1z_2)=Lnz_1+Lnz_2$
$Ln(\frac{z_1}{z_2})=Lnz_1-Lnz_2(z_2\neq0)$
在原点和负实轴上不解析
$Ln(z)^{\prime}=\frac{1}{z}$

幂函数¶

$\Large w=z^\mu=e^{\mu Ln\ z}=e^{\mu ln\ z}·e^{2k\pi \mu i},\mu \in C$

幂函数的求导公式：$(z^\mu)^\prime=\mu z^{\mu-1}$

$w=z^a$ 的多值性

$a$ 为整数——单值函数（左因式为主值，右因式为定值1）
$a$ 为 $p/q$——有限值函数；特别地，$a$ 为 $1/n$ —— $n$ 值函数
$a$ 为无理数/虚部不为0的复数——无穷多值

在原点和负实轴上不解析（可以看作指数函数和对数函数的复合函数）

三角函数和双曲函数¶

$\Large \sin z =\frac{e^{iz}-e^{-iz}}{2i}$
$\Large \cos z =\frac{e^{iz}+e^{-iz}}{2}$
$\Large sh z=\frac{e^z-e^{-z}}{2}$
$\Large ch z=\frac{e^z+e^{-z}}{2}$

在整个复平面上处处解析（可以看作指数函数的复合函数）

和角公式

$\Large ch(a+b)=cha\ chb+sha\ shb$
$\Large sh(a+b)=sha\ chb+cha\ shb$

性质

$\sin z,\cos z$是以$2\pi$为周期的周期函数；$sh z,ch z$是以$2\pi i$为周期的周期函数
$\sin z,sh z$为奇函数；$\cos z,ch z$为偶函数
一些恒等式仍然成立：
- 具体需要额外注意的是：
  - $ch^{2}z - sh^{z} = 1, sh z + ch z = e^{z}$
  - $sh(z_{1} +z_{2})=sh z_{1}ch z_{2}+ ch z_{1}sh z_{2}$
  - $ch(z_{1} +z_{2})=ch z_{1}ch z_{2}+ sh z_{1}sh z_{2}$
与三角函数的关系：
- $sh\ iz=isinz$
- $ch\ iz=cosz$
- $sin\ iz=ishz$
- $cos\ iz=chz$
$|\sin z|\ |\cos z|$不是有界函数