Chapter 1 预备知识¶

约 509 个字 2 张图片预计阅读时间 2 分钟

复数基本知识¶

$z=x+iy=re^{i\theta}$

实部和虚部都相等

$r=\sqrt{x^2+y^2}=|z|$

$\ \theta=Arg\ z = arg\ z +2k\pi$; 是一个集合，每个元素相差 $2\pi$

其中在$(-\pi,\pi]$的 $\theta _{0} \ =\ arg \ z$ 称为辐角主值

辐角主值

$\theta _{0} \ =\ arg \ z \in(-\pi,\pi]$
$arg\ 0,arg\ \infty$ 无意义
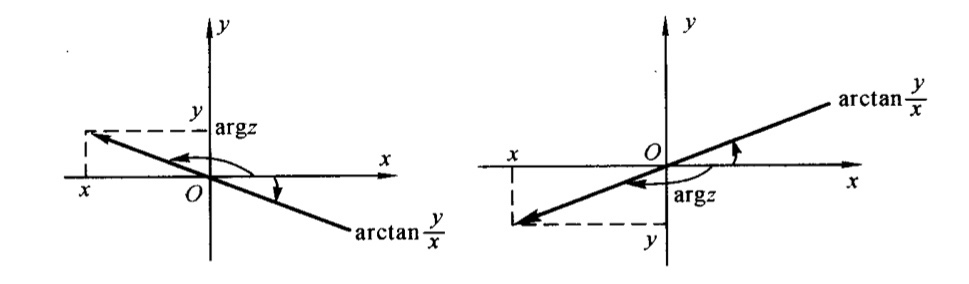
辐角主值可以直接看成平面上的点的对应角，而$arctan\ \frac{y}{x}$∈$(-\frac{\pi}{2},\frac{\pi}{2})$不行。所以二者有一个类似于分段函数的对应关系式

$\Large e^{i\theta}=\cos\theta+i\sin\theta$

复数的加减法——向量的加减法

模长相乘，辐角相加

模长相除，辐角相减

$\left |\frac{z_{1} }{z_{2} } \right | = \frac{\left |z_{1} \right | }{\left |z_{2} \right |} $
$Arg\frac{z_1}{z_2} =Arg \ z_1-Arg \ z_2$

$de Moivre$公式

$\left ( \cos\theta + i\sin \theta \right ) ^{n} \ = \ \cos n\theta + i\sin n \theta$

$\Large z^{n}=r^{n}(\cos n \theta+i \sin n \theta)\ =\ r^{n}e^{in \theta }$

$\Large ^n\sqrt{z}=^n\sqrt{|z|}e^{i\frac{argz+2k\pi}{n}}\ \ k=0,1,\cdots,n-1$

k只取0到n-1的n个值，这是因为k取其他整数时，得到的值必是上述n个值的重复出现

复变函数的可视化

由于定义域和值域都是二维的，用一幅类似实函数的静态图像完整绘制复变函数需要四维的空间，这是很难理解的。我们换一种方式来可视化复变函数。

复数可以画在复平面上，我们让自变量慢慢移动到应变量的位置，可以绘制出一幅动画。比如说函数 $f(z)=z^2$ 的图像如图1所示：

我们知道，根据复数乘法的运算法则，若 $z=r\angle\theta$ ，则 $z^2=r^2\angle2\theta$ ，你在图中也能看到这种对应关系。图中使用辐角主值$\theta\in(-\pi,\pi]$