信号与系统¶

约 1612 个字 8 张图片预计阅读时间 8 分钟

信号的描述¶

注意连续信号$x(t)$==与离散信号$x[n]$==在表示上的区别

周期信号¶

定义：$x(t)=x(t+mT), m=0,\pm1,\pm2$...，其中最小正值$T$被称为基波周期

别的求法之类的就和高中一样了

奇信号与偶信号¶

即类似奇函数与偶函数

信号都可以分解成奇分量与偶分量之和，且分解的方式是唯一的

其中偶分量为偶（Even）函数，满足$x_e(t)=x_e(-t)$
其中奇分量为奇（Odd）函数，满足$x_o(t)=-x_o(-t)$

并且： $$ x_e(t)=\frac{1}{2}[x(t)+x(-t)]\ x_o(t)=\frac{1}{2}[x(t)-x(-t)] $$ 离散信号也是同理，只不过$(t)$换成了$[n]$ $$ x_e[n]=\frac{1}{2}{x[n]+x[n]}\ x_o[n]=\frac{1}{2}{x[n]-x[n]} $$

功率信号与能量信号¶

一个信号的能量和功率是这样定义的：

设信号$x(t)$为电压或电流
则它在$1\Omega$的电阻上的瞬时功率为：$p(t)=|x(t)|^2$$\longleftarrow$之所以是模的平方，是因为$x(t)$可能是复数

在$t_1\le t\le t_2$内消耗的能量为：$E=\int_{t_1}^{t_2} |x(t)|^2dt$

当$T=(t_2-t_1)\longrightarrow \infty$时，总能量$E$和平均功率$P$分别定义为：

\[ E=\lim_{t_2-t_1 \to \infty} \int_{t_1}^{t_2} |x(t)|^2dt\\ P=\lim_{t_2-t_1 \to \infty} \frac{1}{t_2-t_1}\int_{t_1}^{t_2} |x(t)|^2dt \]

在$n_1\le n\le n_2$内的离散时间信号的总能量和平均功率是

\[ E=\sum_{n=n_1}^{n=n_2} |x[n]|^2\\ P=\frac{1}{n_2-n_1+1} \sum_{n=n_1}^{n=n_2} |x[n]|^2 \]

在无穷大区间内，离散时间信号总能量$E$和平均功率$P$分别定义为

\[ E_{\infty}=\lim_{n \to \infty}\sum_{n=-N}^{N} |x[n]|^2=\sum_{n=-\infty}^{\infty} |x[n]|^2\\ P_{\infty}=\lim_{n \to \infty}\frac{1}{2N+1}\sum_{n=-N}^{N} |x[n]|^2 \]

能量信号（能量有限信号）¶

信号$x(t)$的能量$E$满足：$0<E<\infty$，而==$P=0$==

功率信号（简称能量信号）¶

信号$x(t)$的功率$P$满足：$0<P<\infty$，而==$E=\infty$==

常用的公式¶

欧拉公式¶

\[ e^{j\omega _0t}=cos(\omega _0t)+jsin(\omega _0t)\\ cos(\omega _0t)=\frac{1}{2}(e^{j\omega _0t}+e^{-j\omega _0t})\\ sin(\omega _0t)=\frac{1}{2}(e^{j\omega _0t}-e^{-j\omega _0t}) \]

积化和差&和差化积¶

\[ \begin{aligned} \sin (\alpha+\beta) & =\sin (\alpha) \cos (\beta)+\cos (\alpha) \sin (\beta) \\ \sin (\alpha-\beta) & =\sin (\alpha) \cos (\beta)-\cos (\alpha) \sin (\beta) \\ \cos (\alpha+\beta) & =\cos (\alpha) \cos (\beta)-\sin (\alpha) \sin (\beta) \\ \cos (\alpha-\beta) & =\cos (\alpha) \cos (\beta)+\sin (\alpha) \sin (\beta) \\ \sin (\alpha) \cos (\beta) & =\frac{1}{2}[\sin (\alpha+\beta)+\sin (\alpha-\beta)] \\ \cos (\alpha) \sin (\beta) & =\frac{1}{2}[\sin (\alpha+\beta)-\sin (\alpha-\beta)] \\ \cos (\alpha) \cos (\beta) & =\frac{1}{2}[\cos (\alpha+\beta)+\cos (\alpha-\beta)] \\ \sin (\alpha) \sin (\beta) & =\frac{1}{2}[\cos (\alpha-\beta)-\cos (\alpha+\beta)] \\ \sin ^{2}(\alpha) & =\frac{1}{2}[1-\cos (2 \alpha)] \\ \cos ^{2}(\alpha) & =\frac{1}{2}[1+\cos (2 \alpha)] \end{aligned} \]

连续时间信号¶

单位阶跃信号¶

\[ u(t)=\left\{\begin{matrix} 0\ \ \ t<0\\ 1\ \ \ t>0 \end{matrix}\right. \]

在跳变点$t=0$处无定义

延迟的单位阶跃信号，其表示为：

\[ u(t-t_0)=\left\{\begin{matrix} 0\ \ \ t<t_0\\ 1\ \ \ t>t_0 \end{matrix}\right. \]

利用单位阶跃信号表示矩形脉冲¶

矩形脉冲定义为：$G(t)=u(t)-u(t-t_0)$

用阶跃信号与延迟的阶跃信号之差表示

冲激信号¶

与$u(t)$的关系： $$ u(t)=\int_{-\infty}^{t}\delta(t)dt\ \delta(t)=\frac{du(t)}{dt} $$

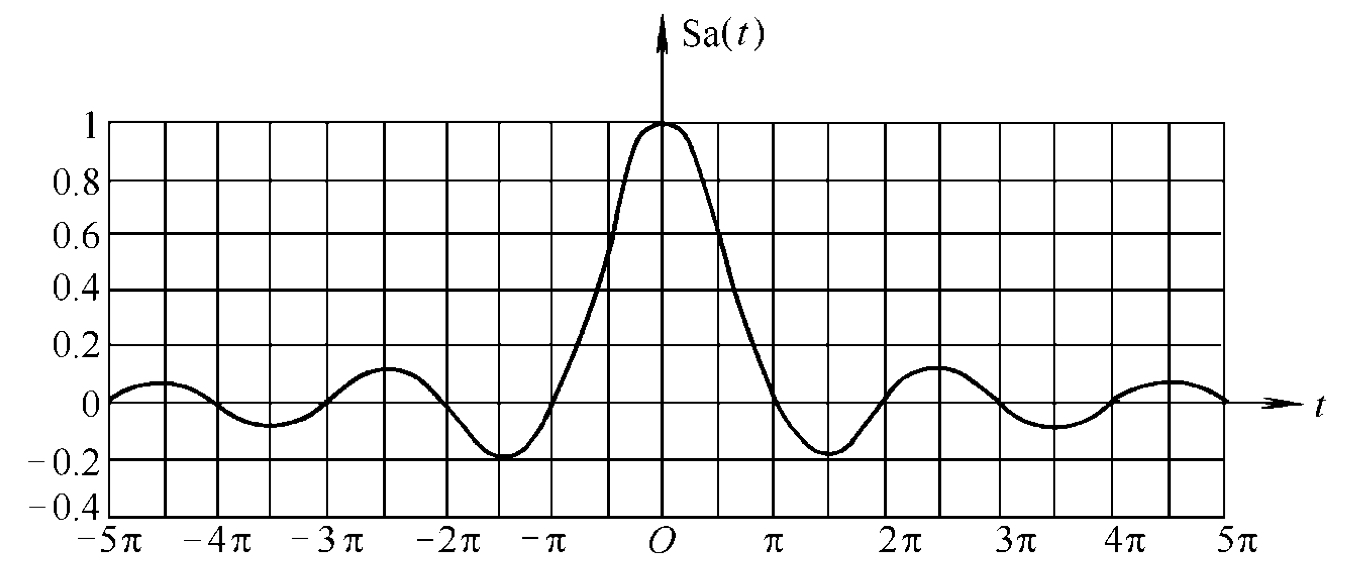
抽样函数¶

定义¶

\[ Sa(t)=\frac{sint}{t}\ or\ sinc(t)=\frac{sin\pi t}{\pi t} \]

性质¶

\[ \int_{-\infty}^{+\infty}Sa(t)=\int_{-\infty}^{+\infty}\frac{sint}{t}dt=\pi\\ \int_{0}^{+\infty}Sa(t)=\int_{-\infty}^{0}\frac{sint}{t}dt=\frac{\pi}{2}\\ \int_{-\infty}^{+\infty}\frac{sin(\omega_0t)}{t}dt=\left\{\begin{matrix} \pi\ \ \ \ \omega_0>0\\ -\pi\ \ \ \omega_0<0 \end{matrix}\right. \]

离散时间信号¶

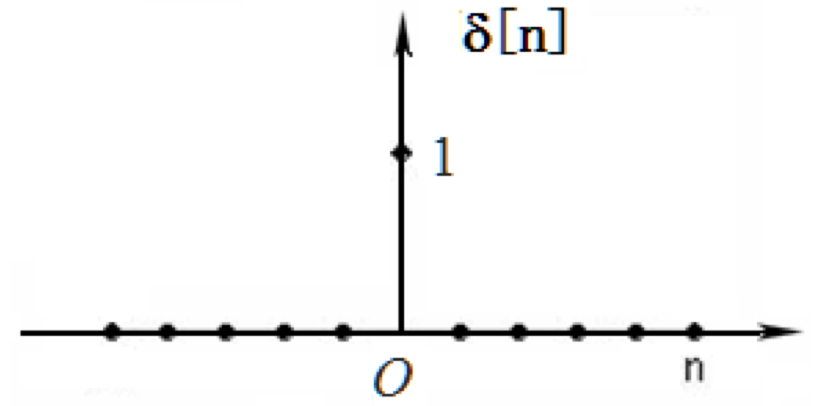
单位冲击序列¶

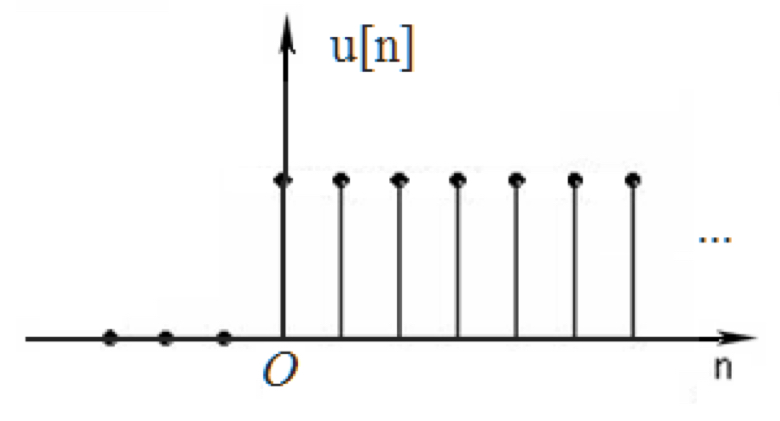
\[ \delta[n]=\left\{\begin{matrix} 0\ \ \ n\ne0\\ 1\ \ \ n=0 \end{matrix}\right. \]

单位阶跃序列¶

\[ u[n]=\left\{\begin{matrix} 0\ \ \ n<0\\ 1\ \ \ n\ge0 \end{matrix}\right. \]

一些公式¶

\[ u[n]=\sum_{k=0}^{\infty} \delta[n-k]=\sum_{k=-\infty}^{n} \delta[k] \\ x[n] \delta[n]=x[0] \delta[n] \\ x[n] \delta\left[n-n_{0}\right]=x\left[n_{0}\right] \delta\left[n-n_{0}\right] \\ \delta[n]=u[n]-u[n-1]\\ x[n]=\sum_{k=-\infty}^{+\infty}x[k]\delta[n-k] \]

其中$x[k]$为$n=k$时，$x[n]$的值；$\delta[n-k]$在$n=k$时值为1，在$n\ne k$时值为0

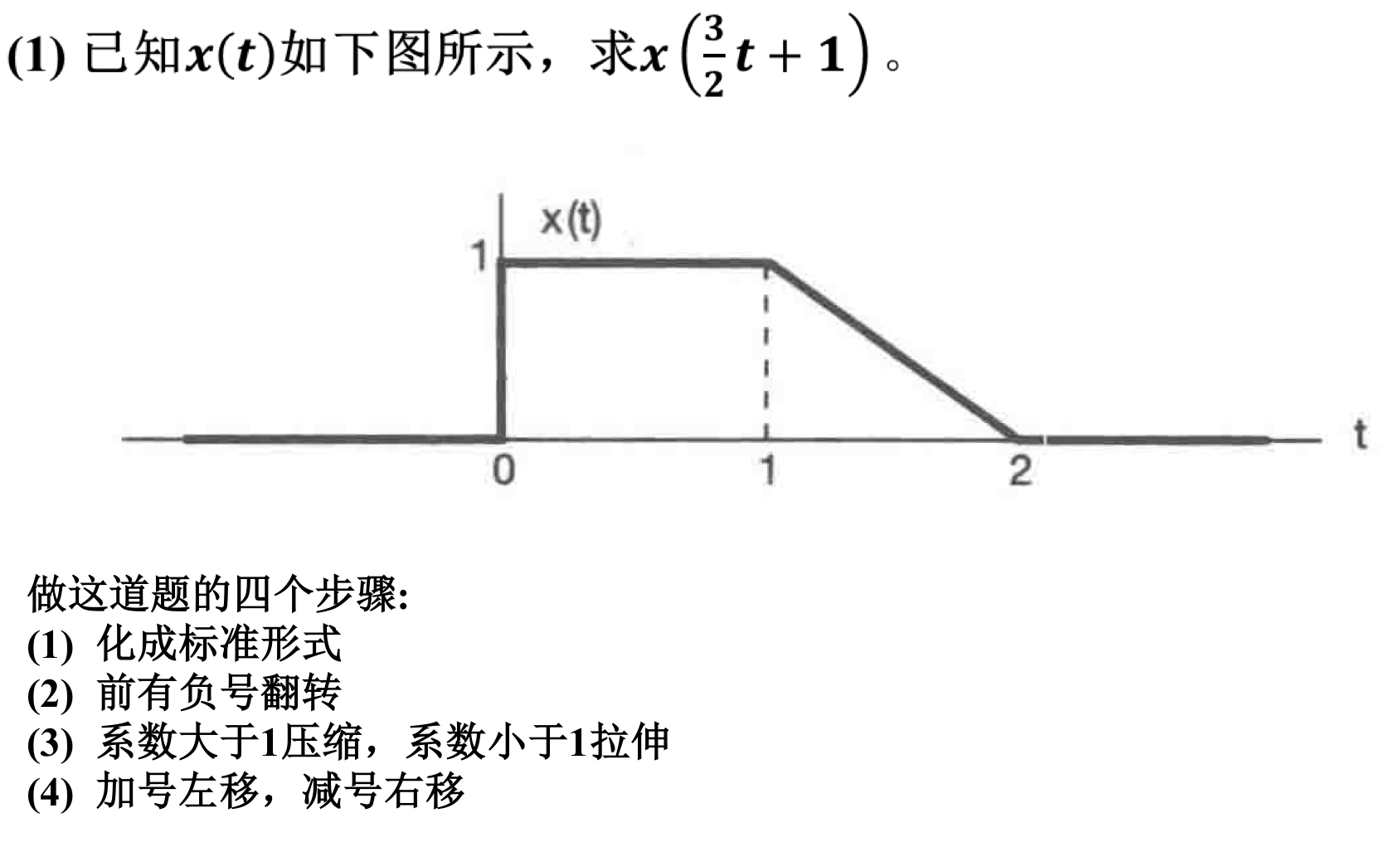
信号的运算与自变量变换¶

个人认为是高中题

系统的基本性质¶

线性系统与非线性系统¶

性质（需要同时满足）¶

齐次性：

如果$\forall x(t)\rightarrow y(t)$，那么对$\forall a \in R$，都有$ax(t)\rightarrow ay(t)$

叠加性：

如果$\forall x_1(t)\rightarrow y_1(t)$，$\forall x_2(t)\rightarrow y_2(t)$，那么$\forall x_1(t)+x_2(t)\rightarrow y_1(t)+y_2(t)$

如果一个系统不是线性系统，那么它就是非线性系统

两个线性系统的串联仍是线性系统，两个线性系统的并联仍是线性系统

线性系统判据：每一项都有x，每一项x的系数都是1

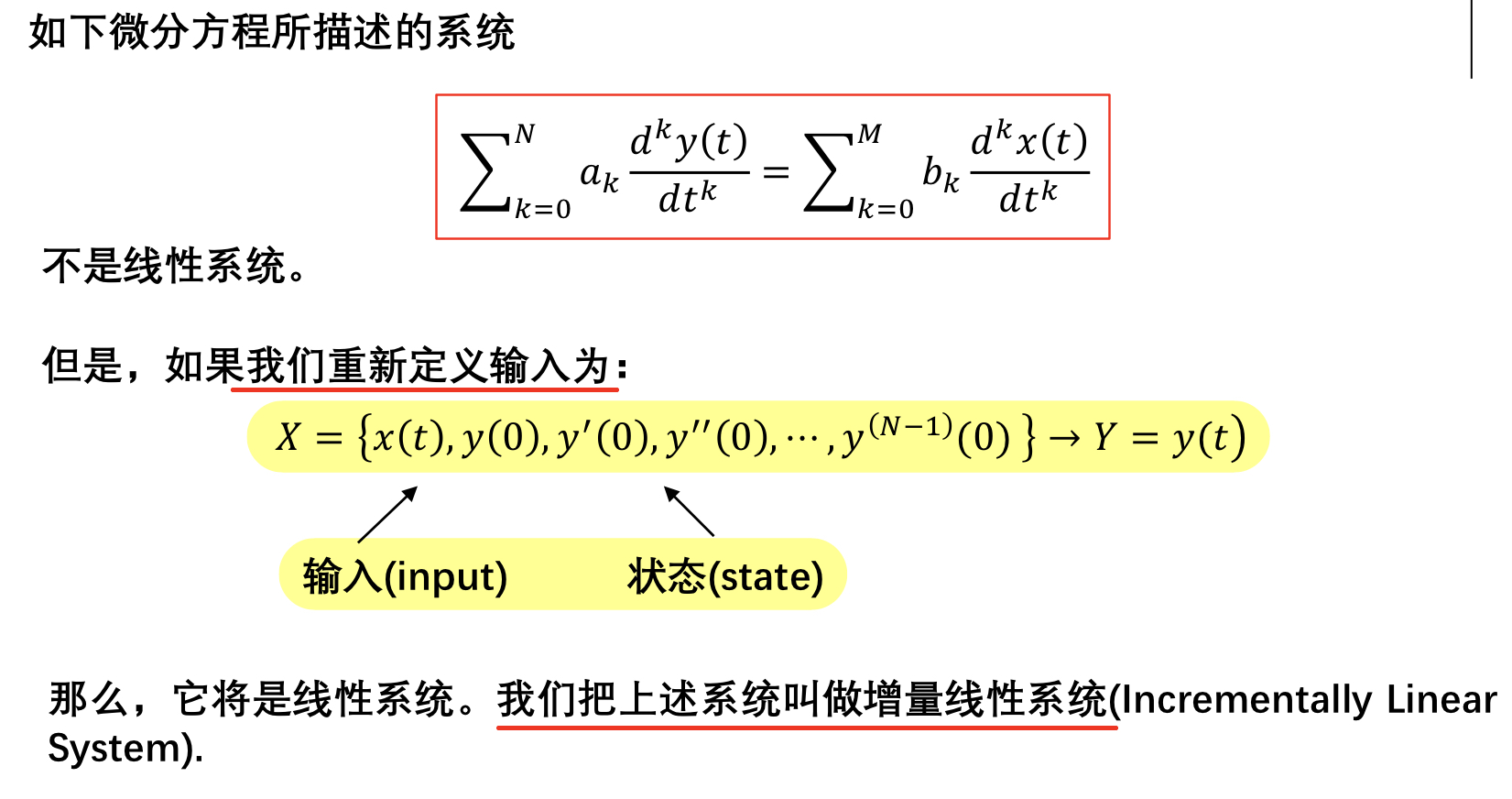
增量线性系统¶

时不变系统¶

性质¶

如果$\forall x(t)\rightarrow y(t)$，那么对$\forall t_0 \in R$，都有$x(t-t_0)\rightarrow y(t-t_0)$。即系统的输出不受时间的影响

两个时不变系统串联仍是时不变系统，两个时不变系统并联仍是时不变系统

时不变系统判据：所有$t$都在$x$的括号内，所有$t$只能是$t$

记忆系统与无记忆系统¶

如果一个系统的输出==仅仅决定于该时刻的输入==，则该系统称为无记忆系统

无记忆系统判据：$y$括号里和$x$括号里一样

因果系统与非因果系统¶

如果一个系统在任何时刻的输出只决定于现在以及过去的输入，而与系统以后的输入无关，就称该系统为因果系统

非因果性就意味着系统不可实现性

因果系统判据：$y$括号里小于等于$x$括号里（所有无记忆系统都是因果系统）

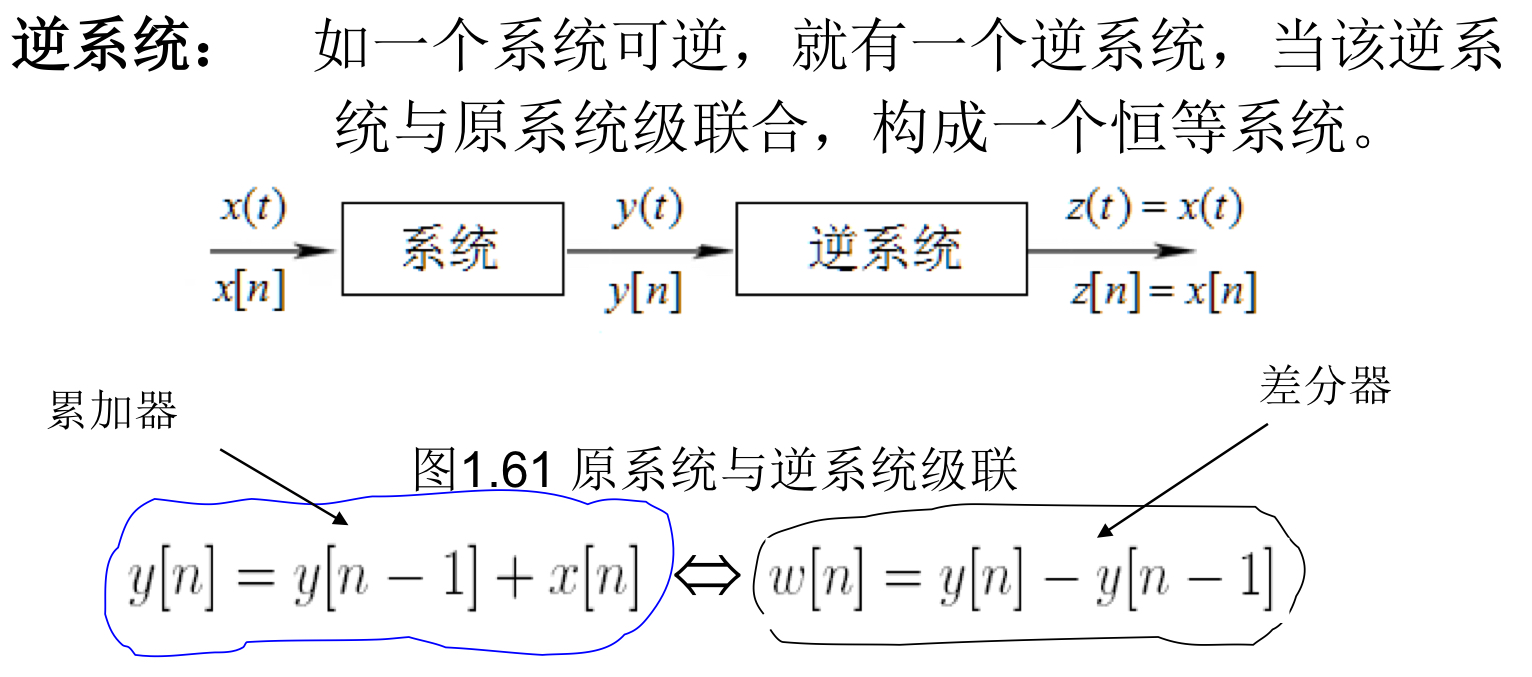
可逆系统与不可逆系统¶

就是相当于函数与反函数

可逆性：不同的输入下有不同的输出
不可逆性：一个系统分别对两个或两个以上不同的输入，能产生相同的输出

系统的稳定性¶

稳定性：输入是有界的，则系统的输出也必须是有界的

系统性质判定

线性系统：

判据：每一项都有$x$，每一项$x$的次数都是 1

时不变系统：

判据：所有$t$都在x的括号()或[]内，所有$t$只能是$t$

因果系统：

判据：与以后的输入无关，决定于现在以及过去（可以仅有其中一个）

无记忆系统：

判据：$y$中的和$x$中的一样，仅仅取决于现在时刻

可逆系统：

判据：不同的输入有不同的输出，感觉和高中的可逆函数差不多

稳定系统：

判据：输入有界时，输出也是有界的