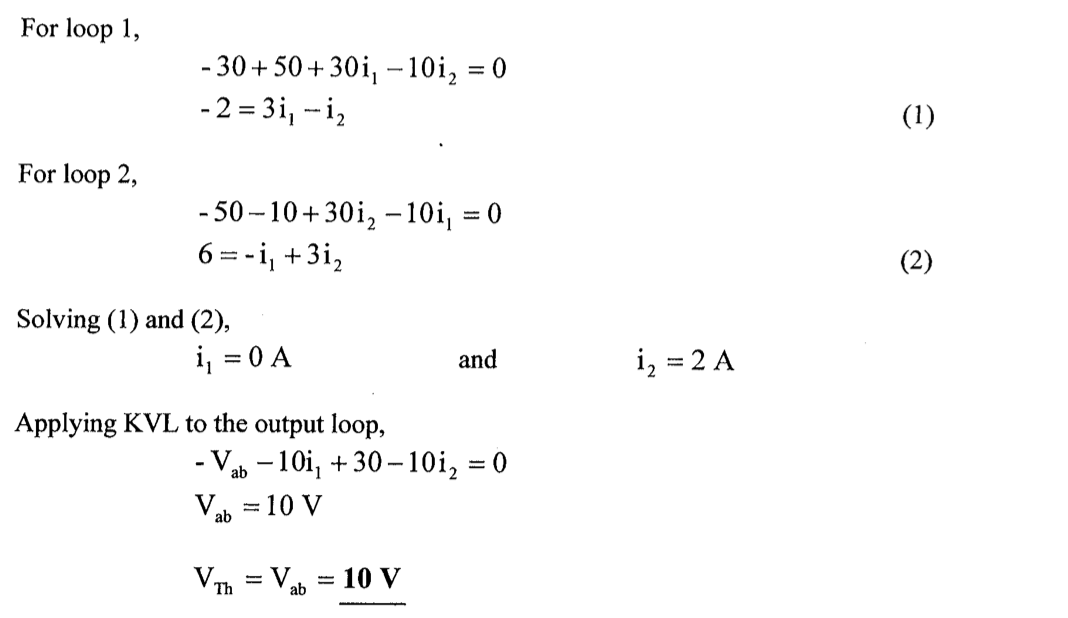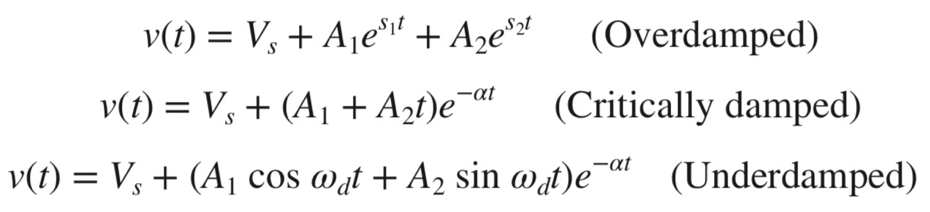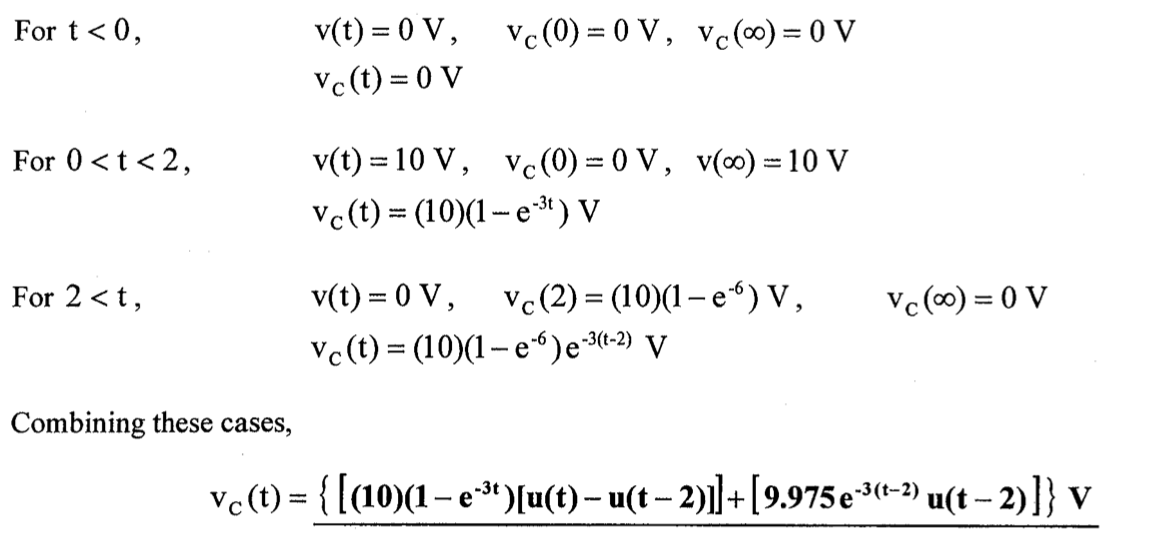跳转至

电子电路基础网站习题集萃

约 5554 个字 57 张图片 预计阅读时间 19 分钟

电路的等效变换部分

核心知识要点

电路的等效计算

电路等效计算：即输入电阻/等效电阻计算（针对一端口网络）

  • 若仅含电阻，等效化简即可
  • 若==含受控源，但不含独立源==，施加电压求电流，或者施加电流求电压
  • 若==含独立源==，则先将其 turn off（电压源短路，电流源开路），再计算

Y-Δ等效变换

Y-Δ等效变换 * \(\Delta\) to Y: \(\Large \frac{相邻之积}{周长之和}\) * Y to \(\Delta\): \(\Large \frac{两两相乘之和}{对面电阻}\) * \(\Delta\) 阻值比较大，更像并联；Y 阻值比较小，更像串联；当阻值相等时，\(\Large R_{\Delta} = 3R_Y\)

题目精选

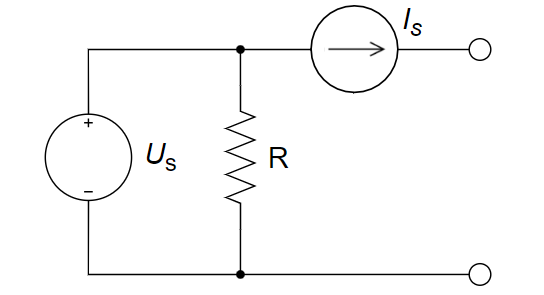
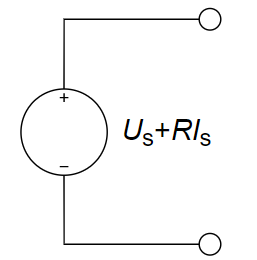
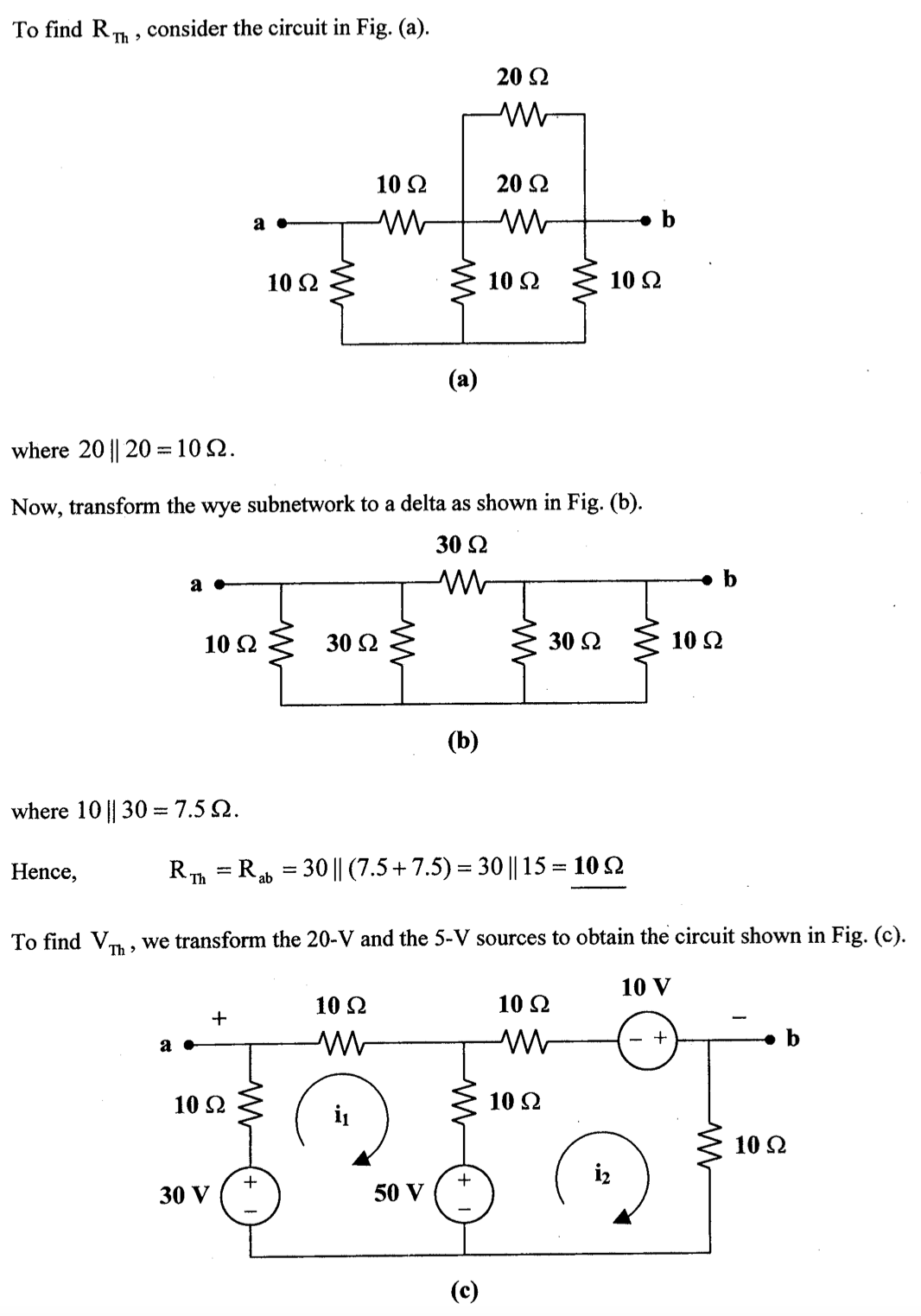
下图所示电路的等效电路为 ________ 。

2-1-5-0

A. 2-1-5-A

B. 2-1-5-B

C. 2-1-5-C

D. 2-1-5-D

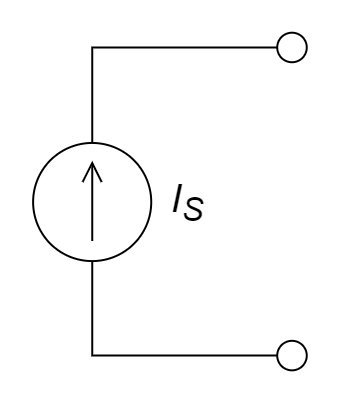
A

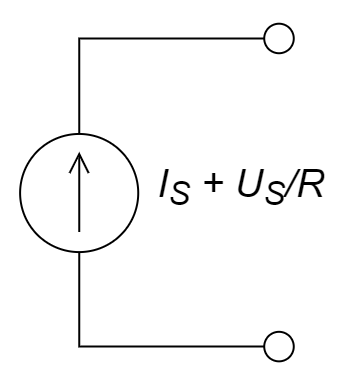
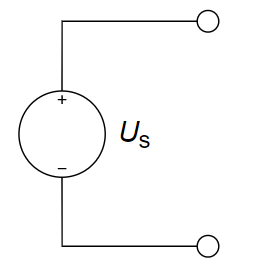
与理想电压源并联的电阻无效（因为电压恒定，电流不定，所以并联无效），故第一步简化为理想电压源和理想电流源串联；与理想电流源串联的元件无效（因为电流恒定，电压不定，所以串联无效），故第二步简化为单个的理想电流源，所以答案为A

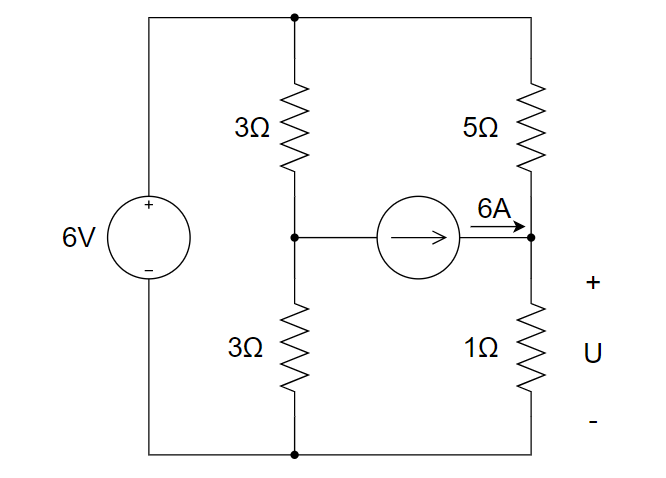
下图所示电路中，电压 U 为 ________ 。

2-2-3

A. \(4V\)

B.\(5V\)

C. \(6V\)

D. \(3V\)

C

对中间右边节点列\(KCL\)，则(6-U)/5 + 6 = U/1，解得U= \(6V\)

这题主要是如何找到合适的节点列\(KCL\)

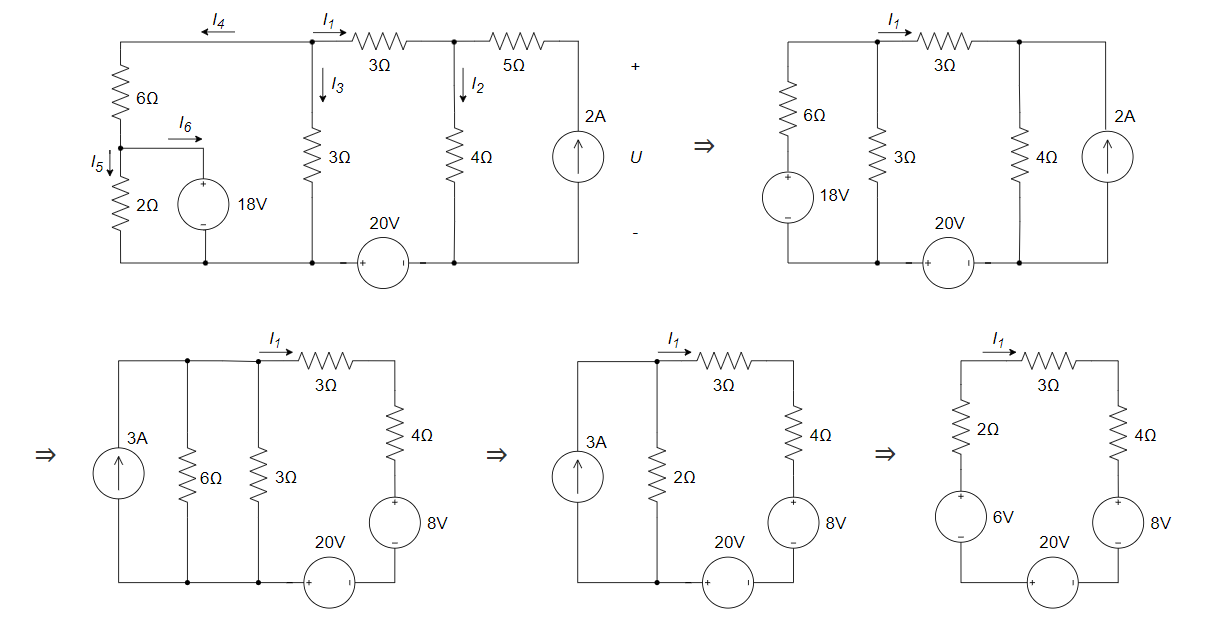
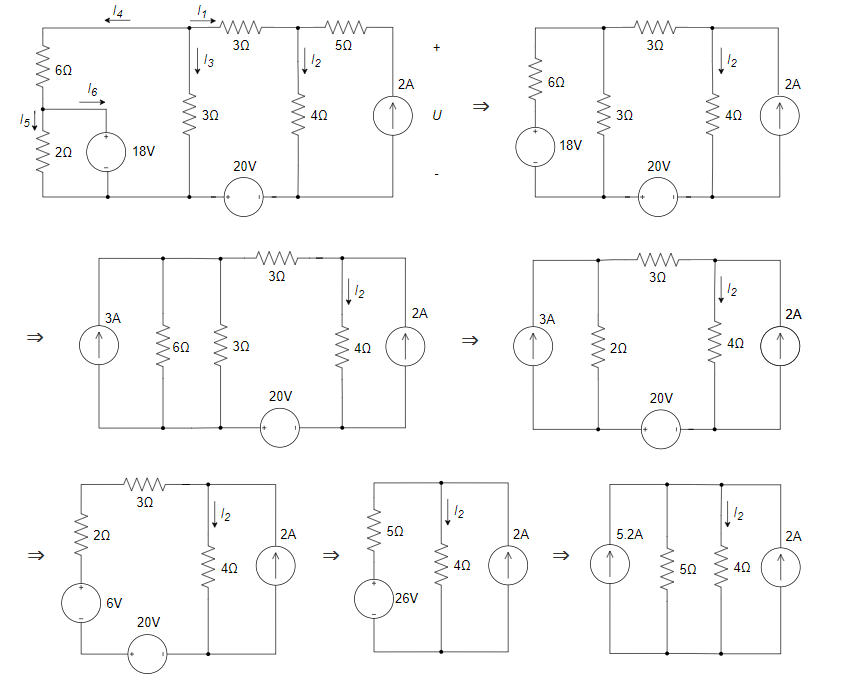
求下图所示电路中电流 \(I_1\) 和 \(I_2\) ，并计算各电源的功率，同时判断该电源是吸收还是发出功率。

2-2-6

方法一：（暴力列\(KCL\)与\(KVL\)求解）

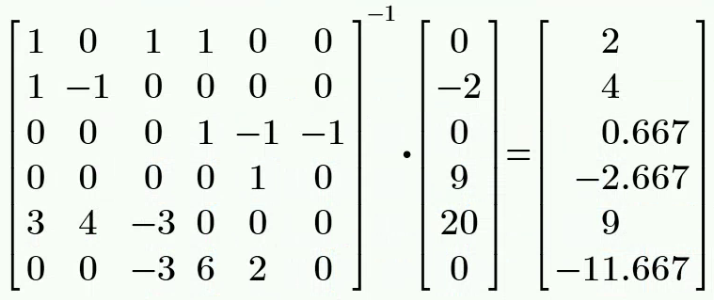
根据各电流量之间的关系、18 V 和 20 V 电压源在负载上的电压降关系，以及左侧大回路的回路电压降关系，列方程组如下： $$ \Large \begin{cases} I_1+I_3+I_4=0 (左上节点KCL)\ I_1+2=I_2 (右上节点KCL)\ I_4=I_5+I_6 (最左节点KCL)\ I_5=\frac{18}{2} (欧姆定律)\ (-I_3×3)+I_1×3+I_2×4=20 (中间loop KVL)\ I_4×6+I_5×2=I_3×3 (最左loop KVL) \end{cases} $$ 解得： $$ \Large \begin{cases} I_1=2A\ I_2=4A\ I_3=\frac{2}{3}A\ I_4=-\frac{8}{3}A\ I_5=9A\ I_6=-\frac{35}{3}A \end{cases} $$

image-20220830084233037

20 V 电压源的功率为： \(P=(2-I_2)×(20V)=-40W\) ，发出功率（关联参考方向）

2 A 电流源的功率为： \(P=(-2A)×U=(-2A)×(I_2×4Ω+5Ω×2A)=-52W\) ，发出功率（关联参考方向）

18 V 电压源的功率为：\(P=18V×I_6=-210W\) ，发出功率（关联参考方向）

方法二：(等效电路法)

(1) 等效电路（求==\(I_{1}\)==，确保\(I_{1}\)所在支路不被等效）

  • 第一步：电流源串联电阻无效
  • 第二步：电流源并联某个电阻等效于电压源串联某个电阻（电阻大小不变，\(U=IR\)）
  • 第三步：电阻并联等效
  • 第四步：电流源并联某个电阻等效于电压源串联某个电阻（电阻大小不变，\(U=IR\)）

image-20220830074153522

得：\(I_1=\frac{6+20-8}{2+3+4}=2A\)

20 V 电压源的功率为 \(P=-20V×2A=-40W\) ，发出功率

(2) 等效电路（求==\(I_{2}\)==，确保\(I_{2}\)所在支路不被等效）

  • 第一步：电流源并联电阻无效
  • 第二步：电压源串联某个电阻等效于电流源并联某个电阻（电阻大小不变，\(U=IR\)）
  • 第三步：电阻并联等效
  • 第四步：电流源并联某个电阻等效于电压源串联某个电阻（电阻大小不变，\(U=IR\)）
  • 第五步：电压源串联等效
  • 第六步：电压源串联某个电阻等效于电流源并联某个电阻（电阻大小不变，\(U=IR\)）

image-20220830074219059

得：\(I_2=\frac{5}{5+4}×(5.2+2)=4A\)

原电路 \(U=5×2+4×4=26V\)

2 A 电流源的功率为 \(P=(-2A)×26V=-52W\) ，发出功率

(3) 18 V 电压源的功率为

\(∵3×2+4×4-20-3I_3=0,∴I_3=\frac{2}{3}A\) （已知\(I_{1}\)\(I_{2}\)求\(I_{3}\)）

\(∵I_4=-(2+\frac{2}{3})=-\frac{8}{3}A ,I_5=\frac{18}{2}=9A\) （\(I_{4}\)由\(KCL\)求得，\(I_{5}\)由欧姆定律求得）

\(∴I_6=I_4-I_5=-\frac{8}{3}-9=\frac{-35}{3}A\)

\(∴P=18V×I_6=18×(-\frac{35}{3})W=-210W\) ，发出功率

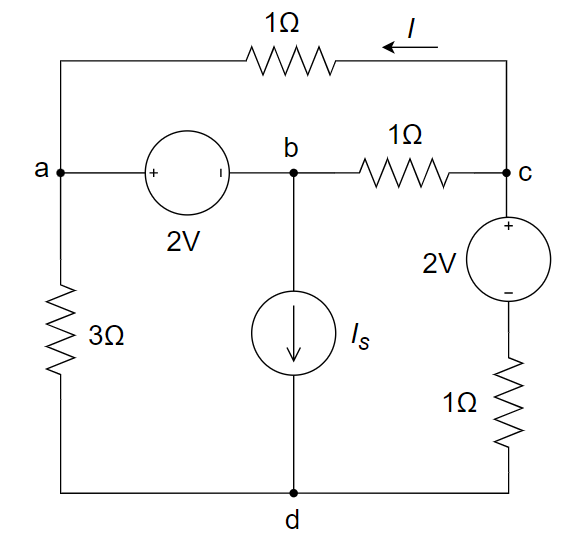
欲使下图所示电路中的支路电流 \(I\) = 1 A，试求电流源的输出电流 \(I_S\) 。

2-2-7

\(V_{ca}=1Ω×1A=1V,V_{cb}=V_{ca}+V_{ab}=1+2=3V,I_{cb}=\frac{V_{cb}}{1Ω}=3A\)

\(I_{dc}=I+I_{cb}=1+3=4A,V_{da}=V_{dc}+V_{ca}=(I_{dc}×1Ω-2V)+V_{ca}=3V\)

\(I_{da}=\frac{V_{da}}{3Ω}=1A,I_s=I_{da}+I_{dc}=1A+4A=5A\)

由果索因，循序渐进

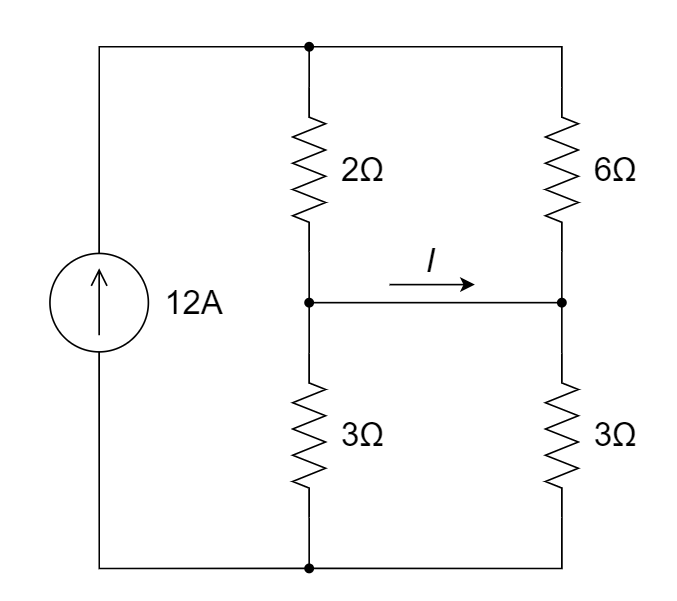
如下图所示电路，支路电流 \(I\) 的值为 ________ 。

2-2-8

3 A

上方两个电阻分流，流过\(2\Omega\)的电流为\(9A\)；下方两个电阻分流，流过左边\(3\Omega\)的电流为\(6A\)，所以\(I=3A\)

这个分流角度去考虑这种电流源的问题还是很有意思的

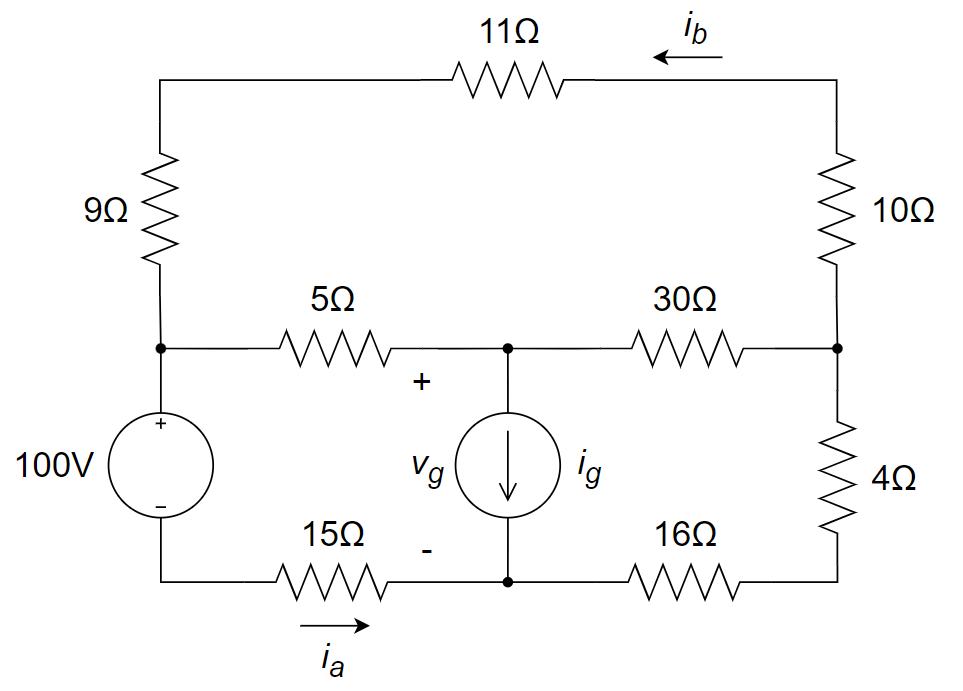
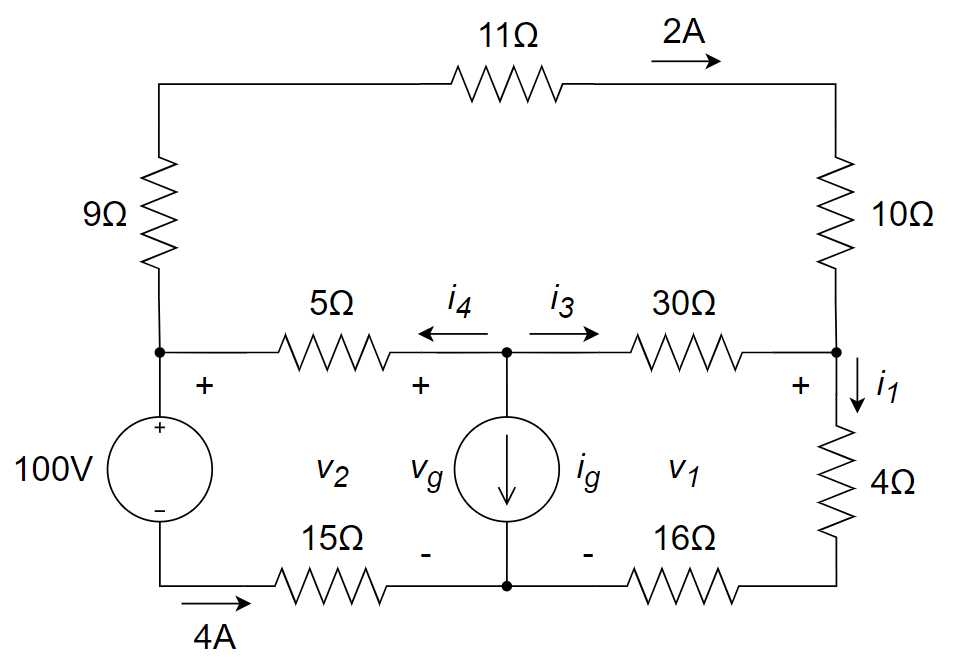
下图所示的电路中的 \(i_a=4{\rm A}\)，\(i_b=-2{\rm A}\)，求：

(1) 电流源的输出电流 \(i_g\)；

(2) 30 Ω 电阻上消耗的功率；

(3) 100 V 电压源提供的功率。

image-20221108121633988

(1)

image-20221108121801834

\(\Large v_2=100+4\times15=160{\rm V}\)（基本的欧姆定律）

\(\Large v_1=160-(9+11+10)\times2=100{\rm V}\) （绕那个大的loop）

\(\Large i_1=\frac{v_1}{4+16}=\frac{100}{20}=5{\rm A}\)（大的求得电压即可求小的电流）

\(\Large i_3=i_1-2=5-2=3{\rm A}\) （最右节点列\(KCL\)）

\(\Large v_g=v_1+30i_3=100+30\times3=190{\rm V}\) （求得\(I_{3}\)即可求电压）

\(\Large i_4=2+4=6{\rm A}\) （最左节点的\(KCL\)）

\(\Large i_g=-i_4-i_3=-6-3=-9{\rm A}\) （中间节点的\(KCL\)）

(2)\(\Large P_{30{\rm \Omega}}=30\times 3^2=270{\rm W}\)

(3)按==关联参考方向==，\(\Large P=100 \times 4=400{\rm W}\)，所以电源==吸收功率 \(400 W\)==

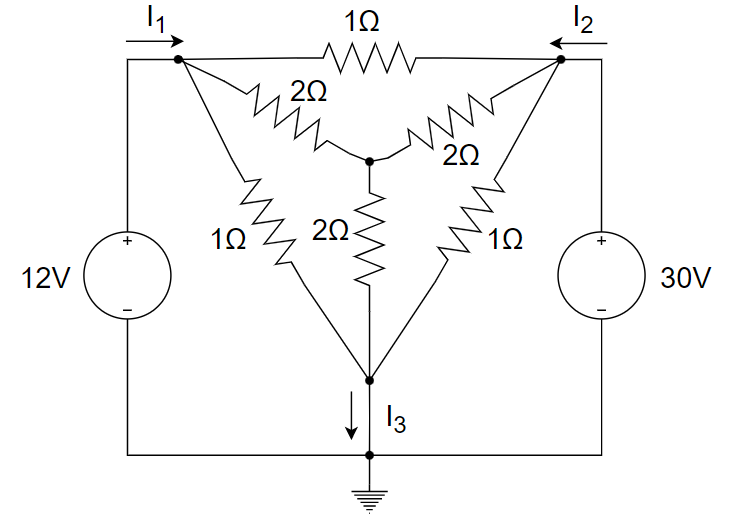
求下图所示电路中的支路电流 \(I_1、I_2和I_3\) 。

2-3-3

\(\Delta\) 阻值比较大，更像并联；Y 阻值比较小，更像串联；当阻值相等时，\(\Large R_{\Delta} = 3R_Y\)

  • \(Z_Y=2Ω\) 变换为 \(Z_Δ=6Ω\)

  • \(6Ω\) 与 \(1Ω\) 并联得到 \(\Large \frac{6}{7}Ω\)

  • 在 \(Δ→Y\) 转换得到 \(\Large \frac{2}{7}Ω\)

通过叠加定理或者网孔电流法可计算得到： $$ \Large \begin{cases}\frac{2}{7}I_1+\frac{2}{7}I_3=12 \\frac{2}{7}I_2+\frac{2}{7}I_3=30 \I_1+I_2=I_3\end{cases}⇒\begin{cases}I_1=-7A \I_2=56A \I_3=49A\end{cases} $$

image-20220830092323304

求下图中每个电容两端的电压

image-20221014142401350

主要就是抓住串联电容的带电量Q是相等的

image-20221014142422374

电路分析方法部分

核心知识要点

电路的分析方法

  • 网孔电流法
    • 以 l 个网孔电流为变量，对 l 个网孔列\(KVL\)方程，求解线性方程组；
    • 若含电流源，因电流源两端电压不能确定，故采用超级网孔避开电流源，再列线性方程求解；
  • 节点电压法
    • 以 n-1 个节点电压为变量，对 n-1 个节点列 n-1 个\(KCL\)方程，求解线性方程组；
    • 若含电压源，因流过电压源的电流不能确定，故采用广义节点把电压源包含进来，再列线性方程组求解；
  • 叠加定理（线性电路齐次性）
    • 线性：齐次性、可加性
    • 功率不可直接叠加
    • 分别计算每个独立源的贡献（考虑一个独立源时，其他独立源均设为零/turn off），再线性叠加；适用于有多个独立源的线性电路
  • 替代定理：保持接口电压或电流不变，用电压源或电流源替代
  • 戴维南定理：开路电压 & 等效电阻
  • 诺顿定理：短路电流 & 等效电阻
  • 最大功率传递定理：
    • 对于电阻网络，负载电阻 = 戴维南等效电阻
    • 最大功率传输时，效率并不一定等于50%

题目精选

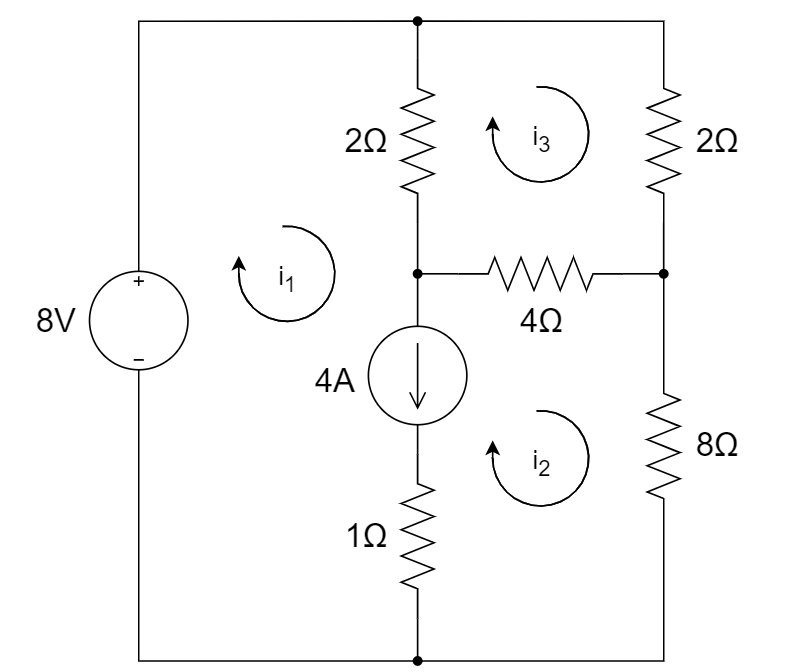
使用网孔电流法求解下图中 \(i_1\)、\(i_2\)、\(i_3\)

image-20220913165141920.BLzr6xZt

考虑到独立电流源的存在，将 \(i_1\) 和 \(i_2\) 所在的网孔并作一个==\(supermesh\)==看待。

列网孔电流方程如下：

\(\Large \begin{cases} -8 +2(i_1-i_3)+4(i_2-i_3) + 8i_2 = 0 \\ 2(i_3-i_1)+2i_3+4(i_3-i_2)=0 \\ \end{cases}\)

增补方程 \(\Large i_1-i_2=4\)

联立解得：

\(i_1=\frac{88}{19}{\rm A},i_2=\frac{12}{19}{\rm A},i_3=\frac{28}{19}{\rm A}\)

用节点电压法求下图所示电路中的电压U

2-5-1.BSvyzG3F

最上方三个节点从左往右依次为\(n1\)、\(n2\)、\(n3\)，节点4即为最下方的节点

  • 第一个方程：电压差
  • 第二个方程：\(n2\)节点的\(KCL\)
  • 第三个方程：电压差（只不过是受控源）
  • 第四个增补方程：欧姆定律

解-2-5-1.BvYfzfhb

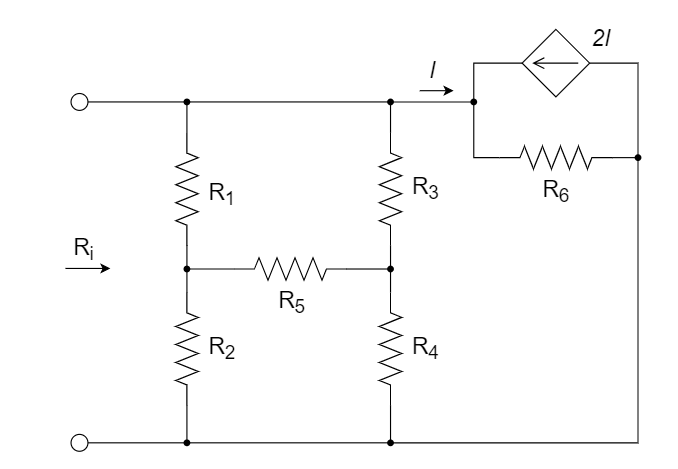
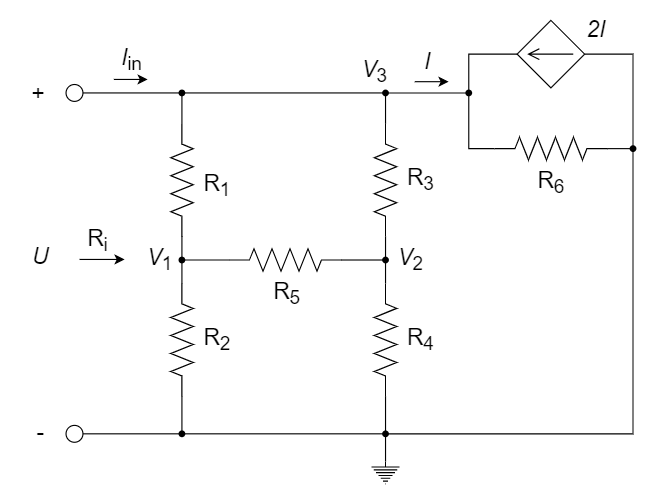
求以下无源单口网络的输入电阻 \(R_i\) 。已知 \(R_1\) = \(R_2\) = \(R_3\) = \(R_4\) = \(R_5\) = 3Ω，\(R_6\) = 1Ω。

2-5-3.aDwYp8PU

方法1：（节点电压法）

选取参考地，并对图中的节点电压进行标记如下：

解-2-5-3.D6OTm7uM

列节点电压方程如下： $$ \Large \begin{cases} V_1/R_2+(V_1-V_2)/R_5+(V_1-V_3)/R_1=0 (对V_1节点的KCL)\ V_2/R_4+(V_2-V_1)/R_5+(V_2-V_3)/R_3=0 (对V_2节点的KCL)\ V_3=3I×R_6 (V_3节点对地电压) \end{cases} $$ 为简化计算过程，可取 \(I=1 A\)（由果索因）

计算得到： \(\Large V_1=V_2=\frac{3}{2}V,V_3=3V,I_{in}=I+V_1/R_2+V_2/R_4=2A\)

故而输入电阻 \(\Large R_i=\frac{U}{I_{in}}=\frac{V_3}{I_{in}}=\frac{3}{2}Ω\)

方法2：（简化电路）

左边电路用Y-\(\Delta\) 化简，等效为3Ω电阻（也可由电桥，\(R_{5}\)不分流，直接是两个\(6\Omega\)电阻并联）

右边电路令\(I = 1A\), 电压\(=3V\)，即右边等效为3Ω，故整体等效电阻为1.5Ω

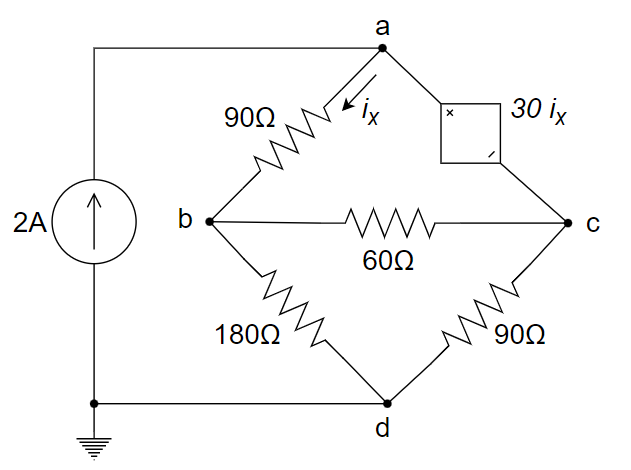
用节点电压法求下图所示电路的节点电压 \(V_{na}、V_{nb}、V_{nc}和i_x\) 。

2-6-7.R-WN5Md-

方法1：

**设受控电压源流出的电流为 \(i\) ** $$ \Large \begin{cases} \frac{1}{90}V_{na}-\frac{1}{90}V_{nb}=2+i (a点KCL)\ -\frac{1}{90}V_{na}+(\frac{1}{90}+\frac{1}{60}+\frac{1}{180})V_{nb}-\frac{1}{60}V_{nc}=0 (b点KCL)\ -\frac{1}{60}V_{nb}+(\frac{1}{90}+\frac{1}{60})V_{nc}=-i (c点KCL)\ V_{na}-V_{nc}=30i_x (受控源列方程)\ i_x=\frac{1}{90}(V_{na}-V_{nb})(i_x的表示 ) \end{cases} $$ 解得： \(\Large V_{na}=135V,V_{nb}=108V,V_{nc}=126V,i=-1.7A,i_x=0.3A\)

方法2： $$ \Large \begin{cases} \frac{1}{90}V_{na}-(\frac{1}{90}+\frac{1}{60})V_{nb}+(\frac{1}{90}+\frac{1}{60})V_{nc}=2 \ 对点b:-\frac{1}{90}V_{na}+(\frac{1}{90}+\frac{1}{60}+\frac{1}{180})V_{nb}-\frac{1}{60}V_{nc}=0 \ 另外,V_{na}-V_{nc}=30i_x=\frac{30}{90}(V_{na}-V_{nb}) \end{cases} $$

$$ ⇒ \Large \begin{cases} 2V_{na}-5V_{nb}+5V_{nc}=360 \ -2V_{na}+6V_{nb}-3V_{nc}=0 \ 2V_{na}+V_{nb}-3V_{nc}=0 \end{cases} ⇒ \Large \left( \begin{matrix} 2 & -5 & 5 \ -2 & 6 & -3 \ 2 & 1 & -3 \end{matrix} \right)

\left( \begin{matrix} V_{na} \ V_{nb} \ V_{nc} \end{matrix} \right) = \left( \begin{matrix} 360 \ 0 \ 0 \end{matrix} \right) $$

解得： $$ \Large \left( \begin{matrix} V_{na} \ V_{nb} \ V_{nc} \end{matrix} \right) = \left( \begin{matrix} 135 \ 108 \ 126 \end{matrix} \right)V,i_x = 0.3 $$

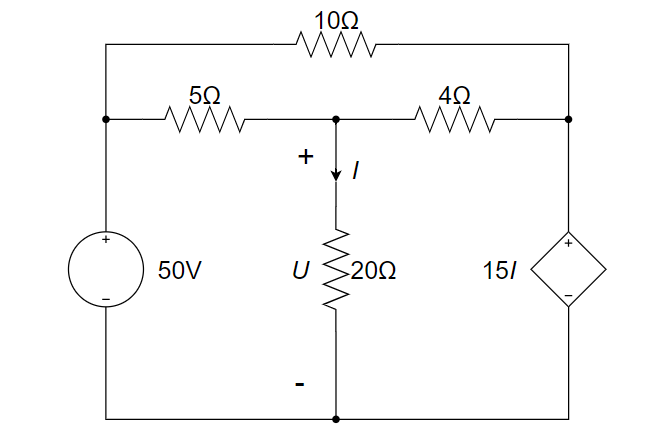
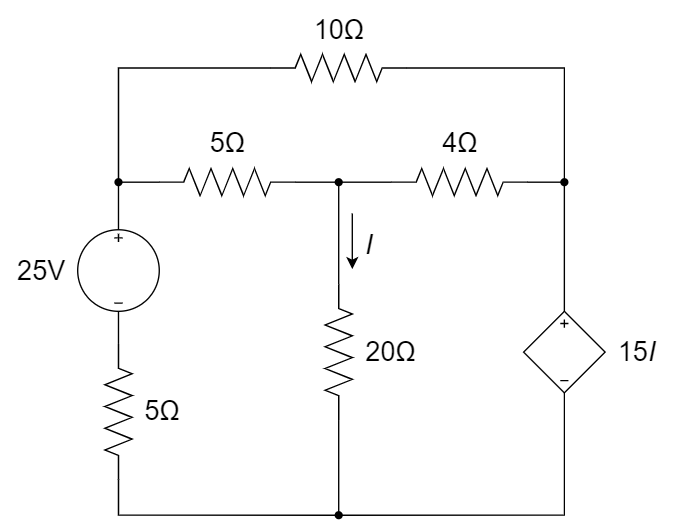
列出图示电路的节点电压方程,并求 \(I\)

2-4-9.9LvruaZ5

独立源 ⇒ \(supernode\)

考虑到独立电压源的存在，将独立电压源及上方节点看做一个 \(supernode\)

记 \(supernode\) 上、下方电压分别为 \(v_a\) 和 \(v_b\)

以底端节点为参考节点，\(supernode\) 右侧的两个节点分别标记为 \(v_1\) 和 \(v_2\)

列节点电压方程如下：

\(\Large \begin{cases} \frac{v_a-v_2}{10}+\frac{v_a-v_1}{5}+\frac{v_b}{5}=0 \\ \frac{v_1-v_a}{5}+\frac{v_1-v_2}{4}+\frac{v_1}{20}=0 \\ v_2=15I \end{cases}\)

增补方程 \(\Large v_a-v_b=25\) ，\(\Large I=\frac{v_1}{20}\)

联立解得：

\(\Large v_a=\frac{1250}{81}{\rm V}\)

\(\Large v_b=\frac{-775}{81}{\rm V}\)

\(\Large v_1=\frac{800}{81}{\rm V}\)

\(\Large v_2=\frac{600}{81}{\rm V}\)

\(\Large I=\frac{40}{81}{\rm A}\)

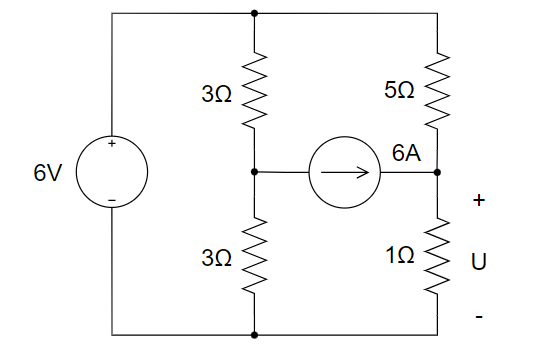
下图所示电路中，电压U为 ________

2-6-2.DPHJCSH9

A. \(4V\)

B. \(5V\)

C. \(6V\)

D. \(3V\)

C

只考虑\(6V\)时，电流源开路，\(U= 1V\)

只考虑\(6A\)时，\(5\Omega\)和\(1\Omega\)并联，\(U\)为\(5V\)

故总的\(U\)为\(1+5=6V\)

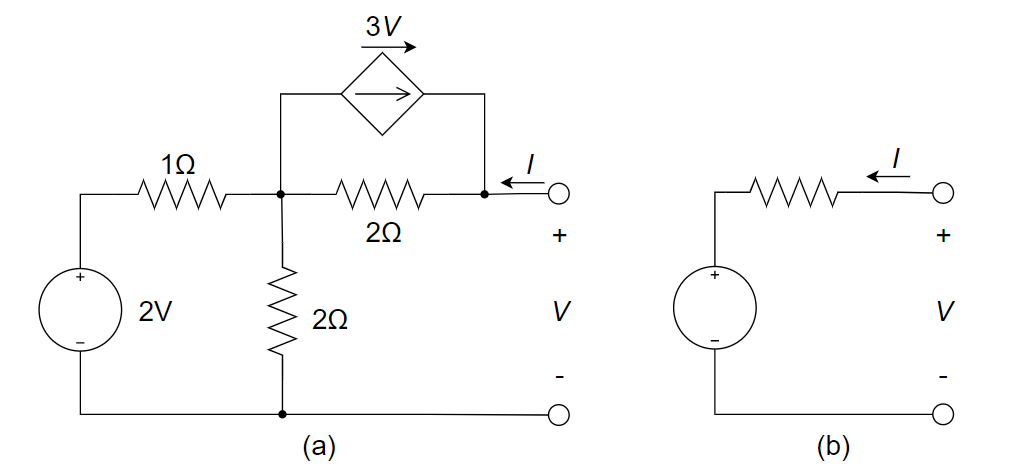
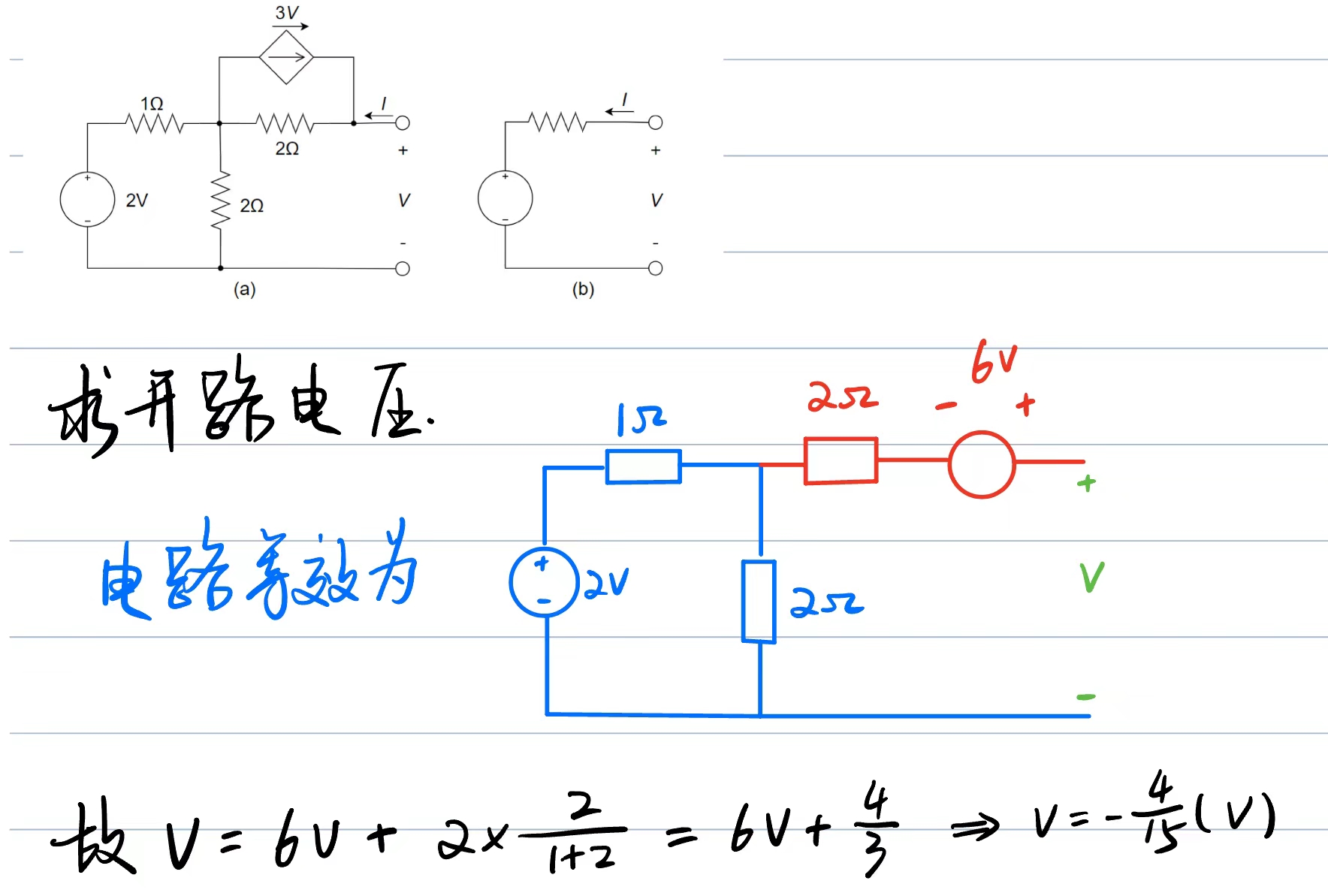
将下图 (a) 电路等效为图 (b) 电路，可求得输出端短路电流 \(I\) = ________

2-7-3.-8HfI5ap

\(-0.5A\)

开路电压：\(\frac{-4}{15}V\)，等效电阻：\(\frac{-8}{15}\ohm\)

微信图片_20241023192058

所以短路电流为 \(-0.5\) A

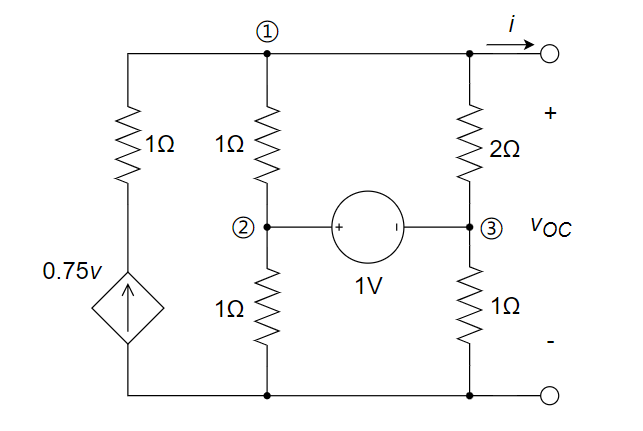
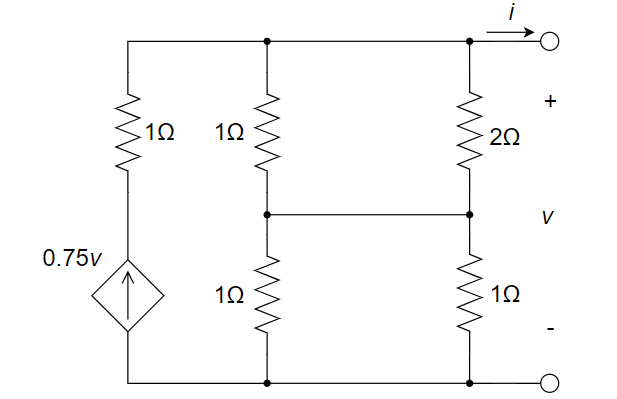
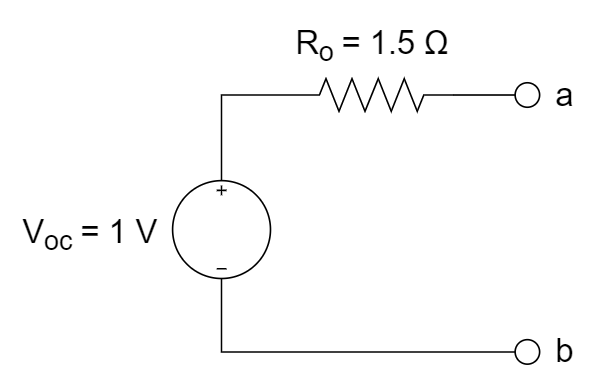
求下图所示电路的戴维南等效电路

1

(1) 首先求开路电压 \(v_{OC}\) 。采用节点分析法来求解

2

$$ \Large \begin{cases} (\frac{1}{1}+\frac{1}{2})v_{OC}-\frac{1}{1}×v_{n2}-\frac{1}{2}×v_{n3}=\frac{3}{4}v_{OC} \ -(\frac{1}{1}+\frac{1}{2})v_{OC}+(\frac{1}{1}+\frac{1}{1})v_{n2}+(\frac{1}{1}+\frac{1}{2})v_{n3}=0 \ v_{n2}-v_{n3}=1 \end{cases} $$ 解得： \(\Large v_{OC}=\frac{4}{3}V≈1.33V\)

(2) 然后求等效电阻 \(R_o\)

​ 在端口施加一电压 \(v\) ，独立电压源短路，与受控电流源串联的电阻可以视为短路，得到：

3

​ 则 \(\Large i=0.75v+\frac{-v}{1Ω||2Ω+1Ω||1Ω}=0.75v+\frac{-v}{\frac{2}{3}+\frac{1}{2}}⇒v=-\frac{28}{3}i\)

​ \(\Large R_o=-\frac{v}{i}=\frac{28}{3}Ω≈9.33Ω\)

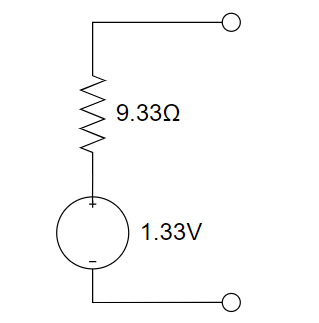
​ 因此，原电路的戴维南等效电路如下所示：

4

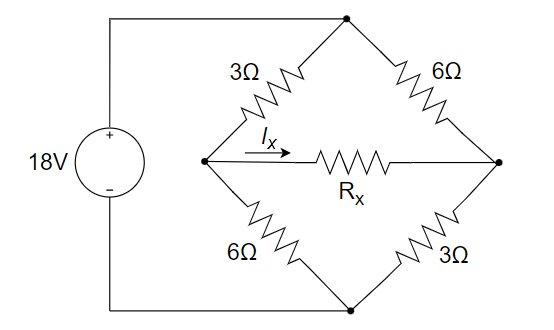
如下图所示电路，当 \(R_x=20Ω\) 时，求电流 \(I_x\)

1

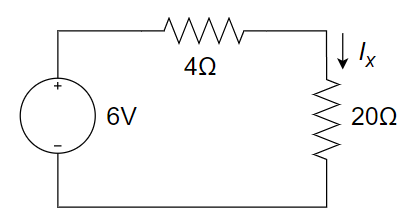
求出 \(I_x\) 所在支路之外电路的戴维宁等效电路。 $$ \Large \begin{cases} u_{oc}=\frac{6}{3+6}×18-\frac{3}{3+6}×18=6V \ R_{eq}=\frac{3×6}{3+6}+\frac{6×3}{6+3}=4Ω \ ∴I_x=\frac{U_{oc}}{R_{eq}+20}=\frac{6}{4+20}=0.25A \end{cases} $$ 等效电路：

2

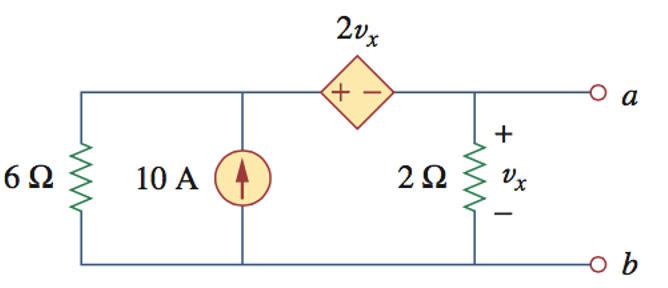
求下图中，ab端所见的戴维南等效电路

1

2

3

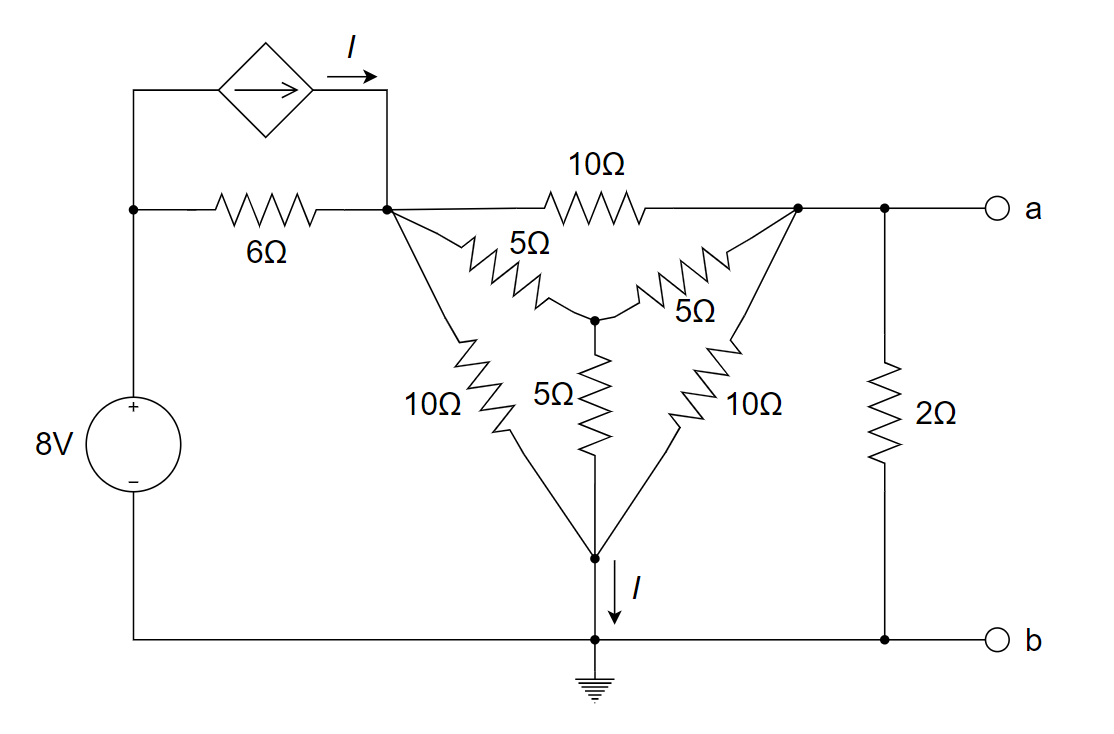
计算并画出下图所示电路的戴维南等效电路

1

首先，根据==\(Y-\Delta\) 变换关系==，且为了方便 \(I\)计算，将\(10\Omega\) 转化为\(\frac{10}{3}\Omega\)，再与 \(5\Omega\) 并联，得到：\({Z_Y}^{'}=2{\rm \Omega}\)

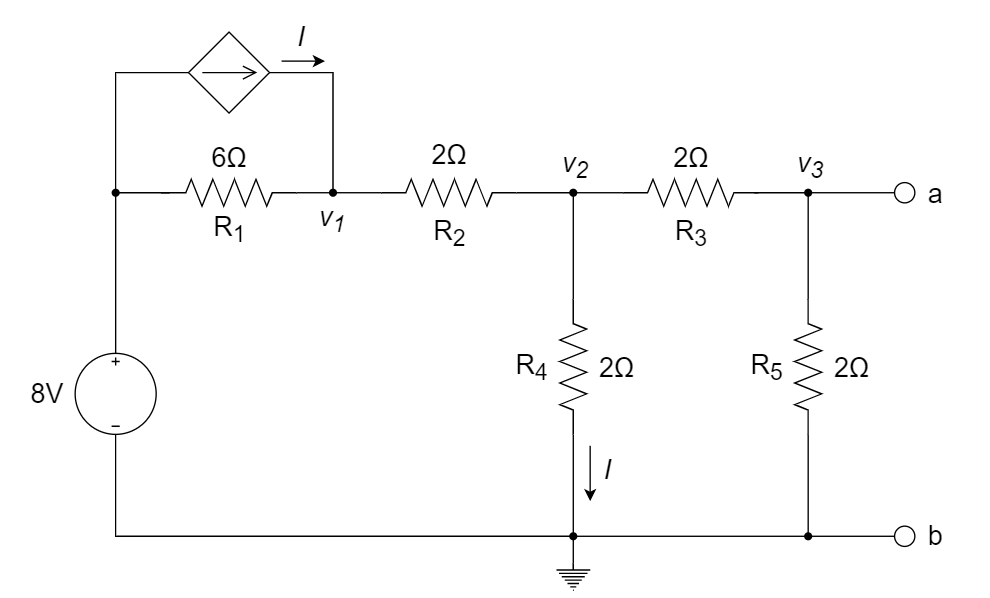
整理得到变换后的电路图如下所示：

2

求开路电压 \(\Large v_{oc}\)

​ 由流经 \(\Large R_4\) 的电流为 \(\Large I\)，可以得到节点2电压为 \(\Large v_2=2I\)

​ 因此，流经 \(\Large R_3\)、\(\Large R_5\) 的电流为 \(\Large 0.5I\)

​ 流经 \(\Large R_2\) 的电流为 \(\Large I+0.5I=1.5I\)；方向由左至右

​ 节点1处由 \(KCL\) 可得，流经 \(\Large R_1\) 的电流为 \(\Large 0.5I\)，方向由左至右

​ 列网孔电流方程有：

​ \(\Large R_1 \times 0.5I+R_2 \times 1.5I + R_4 \times I = 8{\rm V}\)，代入解得：\(\Large I=1{\rm A}\)

​ 开路电压 \(\Large v_{oc}=R_5 \times 0.5I=1{\rm V}\)

求等效电阻 \(\Large R_o\)

​ 在端口施加一电压 \(\Large v=1{\rm V}\)，独立电压源短路

​ 则 \(\Large v_3=1{\rm V}\)，\(\Large v_2=2I\)

​ \(\Large I_{R_5}=\frac{v_3}{R_5}=0.5{\rm A}\)，方向由上至下

​ \(\Large I_{R_3}=\frac{v_3-v_2}{R_3}=\frac{1-2I}{2}=0.5-I\)，方向由右至左

​ \(\Large I_{R_2}=I_{R_3}-I_{R_4}=0.5-2I\)，方向由右至左

​ \(\Large I_{R_1}=I_{R_2}+I=0.5-I\)，方向由右至左

​ 根据 \(\Large v_2=I_{R_2}R_2+I_{R_1}R_1=IR_4\) 代入得到：

​ \(\Large 2 \times (0.5-2I)+6 \times (0.5-I)=2 \times I\)

​ 解得：\(\Large I=\frac{1}{3}{\rm A}\)

​ 因此，\(\Large I_o=I_{R_3}+I_{R_5}=(0.5-\frac{1}{3})+\frac{1}{2}=\frac{2}{3}{\rm A}\)，\(\Large R_o=\frac{v}{I_o}=1.5{\rm \Omega}\)

画出戴维南等效电路如下

3

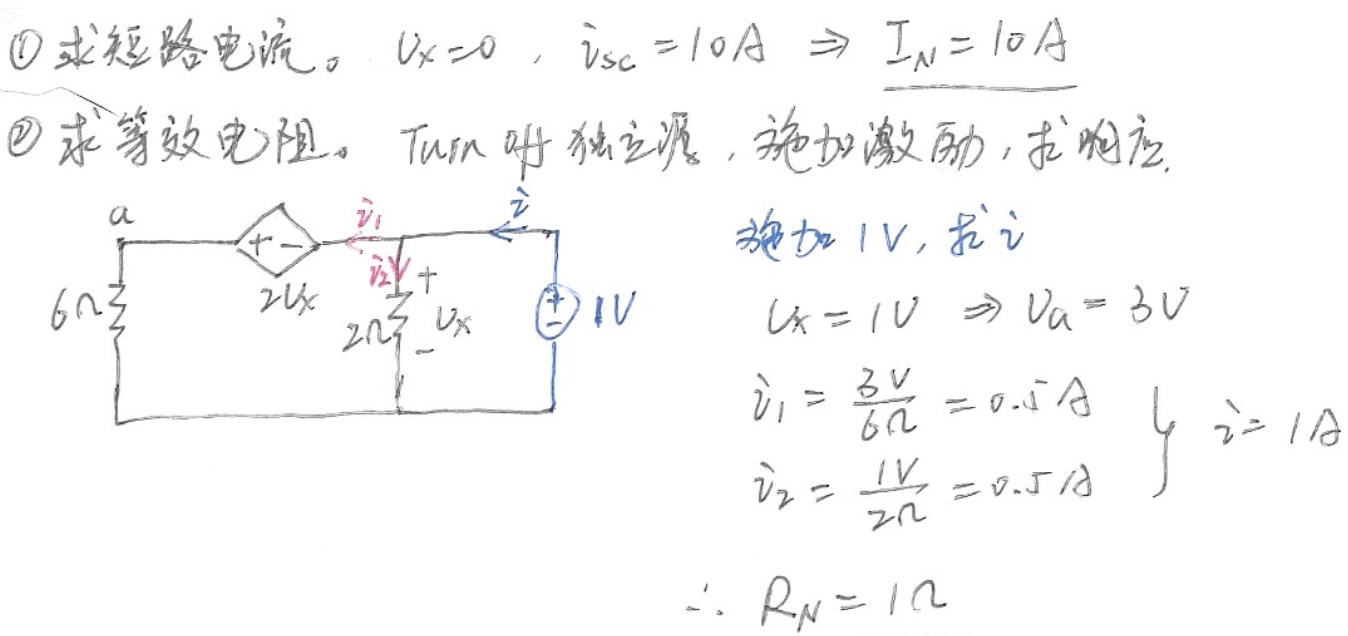
求下列电路\(ab\)端口的诺顿等效电路

1

主要是知道一下诺顿等效怎么求

2

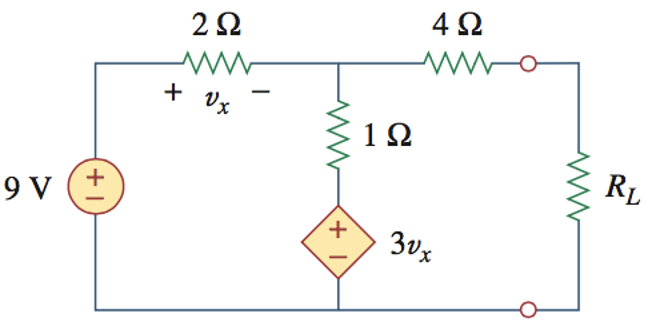
下列电路中，\(R_L\)取什么值时可以获得最大功率传输，并计算该最大功率

1

2

动态电路的时域分析部分

省流

  • 零输入\(RC\)电路
\[ \Large v(t)=V_{0}e^{-\frac{t}{\tau}} \]
  • \(\Large \tau=RC\)
  • \(R\)为\(C\)两端的等效电阻（即戴维南电阻）
  • \(V_{0}\)为\(0+\)时刻电容两端的初始电压
  • 零输入\(RL\)电路
\[ \Large v(t)=I_{0}e^{-\frac{t}{\tau}} \]
  • \(\Large \tau=\frac{L}{R}\)
  • \(R\)为\(L\)两端的等效电阻（即戴维南电阻）

  • $ I_{0}\(为\)0+$时刻流经电感的初始电流I

  • \(RC\)电路的直流响应

\[ \Large v_{c}=V_{s}(1-e^{-\frac{t}{\tau}}) \]

$$ \Large i_{c}=\frac{V_{s}}{R}e^{-\frac{t}{\tau}} $$ * \(\Large \tau=RC\) * \(V_{S}\)电压源电压

[!TIP]

  • \(RL\)电路的直流响应
\[ \Large i_{L}=\frac{V_{s}}{R}(1-e^{-\frac{t}{\tau}}) \]

$$ \Large v_{L}=V_{s}e^{-\frac{t}{\tau}} $$ * \(\Large \tau=\frac{L}{R}\) * \(V_{S}\)电压源电压 [!TIP]

  • 一阶电路的全响应
\[ \Large v_{c}=V_{s}+(V_{0}-V_{s})e^{-\frac{t}{\tau}} \]
  • \(v_{c}(0+)=V_{0}\)
  • \(\Large \tau=RC\)
  • \(V_{S}\)电压源电压

也可写作： $$ \Large v_{c}=V_{s}(1-e{-\frac{t}{\tau}})+V_{0}e $$ 其中 $$ \Large V_{s}(1-e^{-\frac{t}{\tau}}) $$ 为}{\tau}零状态响应 $$ \Large V_{0}e^{-\frac{t}{\tau}} $$ 为零输入响应

  • 一阶电路的三要素法
\[ \Large f(t)=f'(t)+[f(0_{+})-f'(0_{+})]e^{-\frac{t}{\tau}} \]

直流激励时： $$ \Large f'(t)=f'(0_{+})=f(\infty ) $$

\[ \Large f(t)=f(\infty)+[f(0_{+})-f(\infty)]e^{-\frac{t}{\tau}} \]
  • \(\Large f(\infty)\)稳态解（用\(t\longrightarrow \infty\)的稳态电路求解）

  • \(\Large f(0_{+})\)初始解（用\(0_{+}\)等效电路求解）

  • \(RC\)阶跃响应总结

\[ \Large v(t)=v(\infty)+[v(0)-v(\infty)]e^{-\frac{t}{\tau}} \]
  • 若电路是在\(\Large t=t_{0}\)时刻切换
\[ \Large v(t)=v(\infty)+[v(t_{0})-v(\infty)]e^{-\frac{t-t_{0}}{\tau}} \]
  • \(RL\)阶跃响应总结
\[ \Large i(t)=i(\infty)+[i(0)-i(\infty)]e^{-\frac{t}{\tau}} \]
  • 若电路是在\(\Large t=t_{0}\)时刻切换
\[ \Large i(t)=i(\infty)+[i(t_{0})-i(\infty)]e^{-\frac{t-t_{0}}{\tau}} \]

核心知识要点

  • 动态电路和过渡过程的概念

    • 电感、电容的“电压电流约束关系”与时间 t 有关，所以电感、电容又称为动态元件，含电感、电容的电路也被称为动态电路

    • 动态电路的一个特征是：当电路结构发生变化时（一般通过“开关”的切换来实现），可能使电路从原来的工作状态，转变到一个新的工作状态，这种转变往往需要一定的时间，这一过程被称为动态电路的过渡过程

    • 开关切换的动作也被称为“换路”，一般认为换路是在 \(t=0\) 时刻进行的，把换路前的最终时刻记为 \(t = 0^-\)，把换路后的最初时刻记为 \(t = 0^+\)

    • 分析动态电路的方法：根据\(KCL\)、\(KVL\)、元件的电压电流约束关系，写出微分方程，并求解；这一方法在时域中进行，称为经典解法

image-20220905214609711.xX-b-DIV * 一阶电路的响应

* 一阶电路：化简后的电路仅含一个储能元件

* 解一阶微分方程需要知道变量初始值

* $0^+$ 时刻的电路状态由 $0^-$ 时刻的电路状态获得，且基于
    * 电感电流不能突变
    * 电容电压不能突变

* 一阶电路的衰减常数：$\Large \tau = RC$, 或 $\Large \tau = \frac{L}{R}$

  • 零输入响应、零状态响应、全响应及其分解方式、三要素法分析；

    • 输入==指 \(\Large t = 0^+\) 时刻，电路中==有无电源

    • 状态==指 \(\Large t = 0^+\) 时刻，电路中的==储能元件有无初始储能

    • 零输入响应：无外加激励电源（零输入），仅由动态元件初始储能所产生的响应

    • 零状态响应：动态元件初始储能为零（零状态），由外加激励电源引起的响应

    • 实际情况往往是\(t = 0^+\) 时刻==电源和初始储能都有的==，即==全响应==

  • 三要素法：初始值、稳态值、时间常数

  • 初始与稳态的差值随时间常数的指数衰减，所以 $$ \Large v(t) = v(\infty) + [v(t_0) - v(\infty)] \cdot e^{-(t - t_0)/\tau} $$

  • 二阶电路的响应

  • 二阶电路：化简后的电路含两个储能元件

  • 解二阶微分方程需要知道变量初始值，以及变量导数的初始值

  • focus on 不能突变的量，即电感电流、电容电压，寻找变量初始值

    • 变量导数的初始值由元件的外围电路决定

      • 如电感，求电流导数的初始值，因 \(\Large v = L \frac{di}{dt}\) ，需经由电感两端电压初始值获得
      • 如电容，求电压导数的初始值，因 \(\Large i = C \frac{dv}{dt}\)，需经由流经电容电流初始值获得

  • 求解二阶微分方程，即获得二阶电路的解

    • step 1: 求变量及变量导数的初始值
    • step 2: 求微分方程的特解，即变量的稳态响应 \(x_{ss}(t) = x(\infty)\)
    • step 3: \(0^+\) 时刻，turn off 独立源，求齐次微分方程的通解，即变量的瞬态响应 \(x_t(t)\)
    • step 4: 写出非齐次微分方程的通解，即稳态响应和瞬态响应相加 \(x(t) = x_t(t) + x_{ss}(t)\)
    • step 5: 结合初始条件，求待定系数

  • 对于串联 RLC、并联 RLC 这两种特殊的二阶电路，可根据衰减常数和谐振频率直接写出解的表达式

    • 衰减常数，对于串联 \(RLC\)，\(\alpha = \frac{R}{2L}\) ；对于并联 \(RLC\)，\(\alpha = \frac{1}{2RC}\)

    • 谐振频率，\(\omega_0 = \frac{1}{\sqrt{LC}}\)

    • 典型的二阶电路有过阻尼（\(\alpha > \omega_0\)）、临界阻尼（\(\alpha = \omega_0\)）、欠阻尼（\(\alpha < \omega_0\)）三个 cases；临界阻尼衰减最快；以下以电容电压为例

    image-20220905225258656.DiTDYyS5

\[ \Large s_{1,2} = -\alpha \pm \sqrt{\alpha^2 - \omega_0^2} \]
\[ \Large \omega_d = \sqrt{\omega_0^2 - \alpha^2} \]

  • Q：选取电感电流还是电容电压作为变量？A：都可以

    • 有激励时，取激励的量比较方便（即稳态时容易获得的是电压量还是电流量）
    • 无激励时，并联取电压比较方便，串联取电流比较方便

  • 阶跃响应、冲激响应。

  • 单位斜坡函数是单位阶跃函数的积分

  • 单位冲激函数是单位阶跃函数的导数
  • 一阶电路：单位冲激响应可当作电容两端初始电压为1/C （或流经电感的初始电流为1/L）的零输入响应来处理
  • 二阶电路：冲激响应可以按阶跃激励的一阶导数求得

题目精选

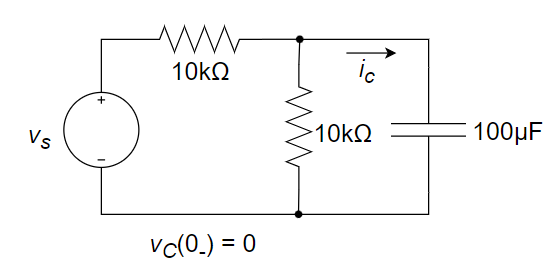
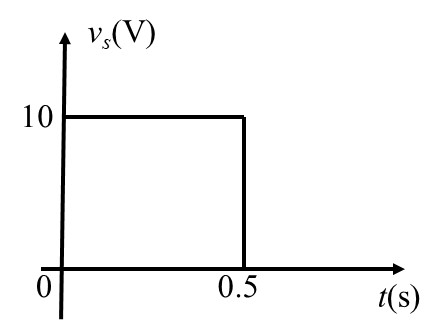
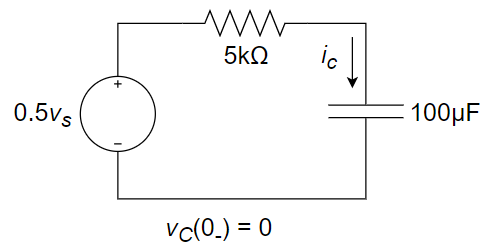
求下左图所示电路中电流 \(i_c(t)\) ，独立电压源的伏安特性曲线见下右图。

1

3

对左侧电路进行戴维南等效，化简电路图如下所示：

2

\[ \Large v_s=10ε(t)-10ε(t-0.5) \]
\[ \Large τ=RC=5×10^{3}×100×10^{-6}=0.5s \]

该电路的单位阶跃响应为 $$ \Large v_C(t)=(1-e^{-2t})ε(t) $$

\[ \Large i_C=C\frac{dv_C}{dt}=\frac{1}{5}e^{-2t}ε(t)(mA) \]

由齐次性和叠加性得实际响应为： $$ \Large i_C=5×[\frac{1}{5}e{-2t}ε(t)-\frac{1}{5}eε(t-0.5)]=e{-2t}ε(t)-eε(t-0.5)(mA) $$

另外，也可以分段表示结果：

\(0<t<0.5,ε(t)=1,ε(t-0.5)=0\) $$ \Large i_C=e^{-2t}(mA) $$ \(t>0.5,ε(t)=1,ε(t-0.5)=1\) $$ \Large i_C=e{-2t}-e=e{-2(t-0.5)}(e(mA) $$ }-1)=-0.632e^{-2(t-0.5)

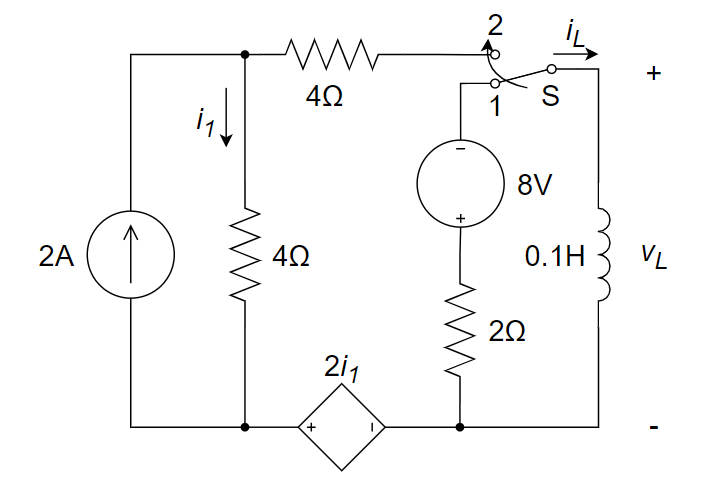
如下图所示电路，在 t = 0 时刻前，开关 S 在位置 1 时电路已达到稳定状态，t = 0 时开关由位置 1 向位置 2闭合，求 t ≥ 0 时的电压 \(v_L\)

4-1-7.Cja6G81L

开关在 1 位置时，\(\Large i_L(0^-)=-4A\)

\(0^+\) 时刻之后，将电感以外电路进行==戴维南等效==，求得：\(\Large v_{oc}=12V，R_{eq}=10Ω\)

时间常数为 \(\Large τ=\frac{L}{R_{eq}}=0.01s\)

边界条件为 \(\Large i_L(0^+)=i_L(0^-)=-4A,i_L(∞)=\frac{v_{oc}}{R_{eq}}=1.2A\)

应用==三要素法==，得到：

​ \(\Large i_L(t)=1.2+(-4-1.2)e^{-\frac{1}{0.01}t}=(1.2-5.2e^{-100t})A\)

​ \(\Large v_L(t)=L\frac{di_L}{dt}=52e^{-100t}V\)

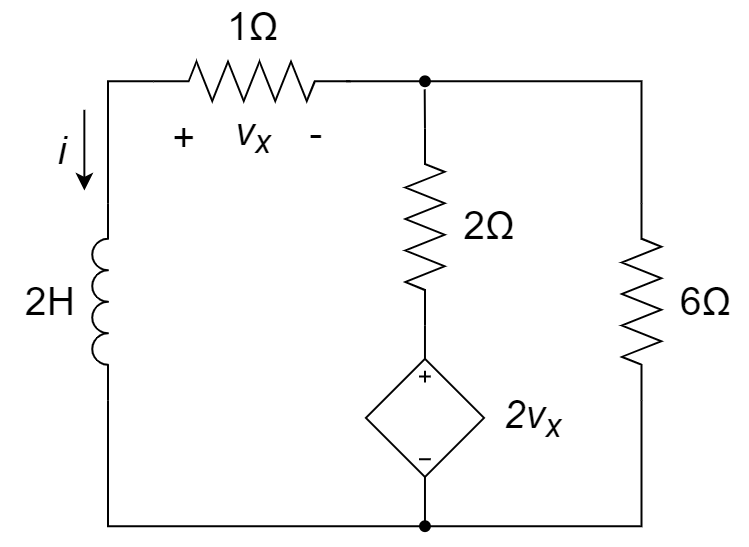
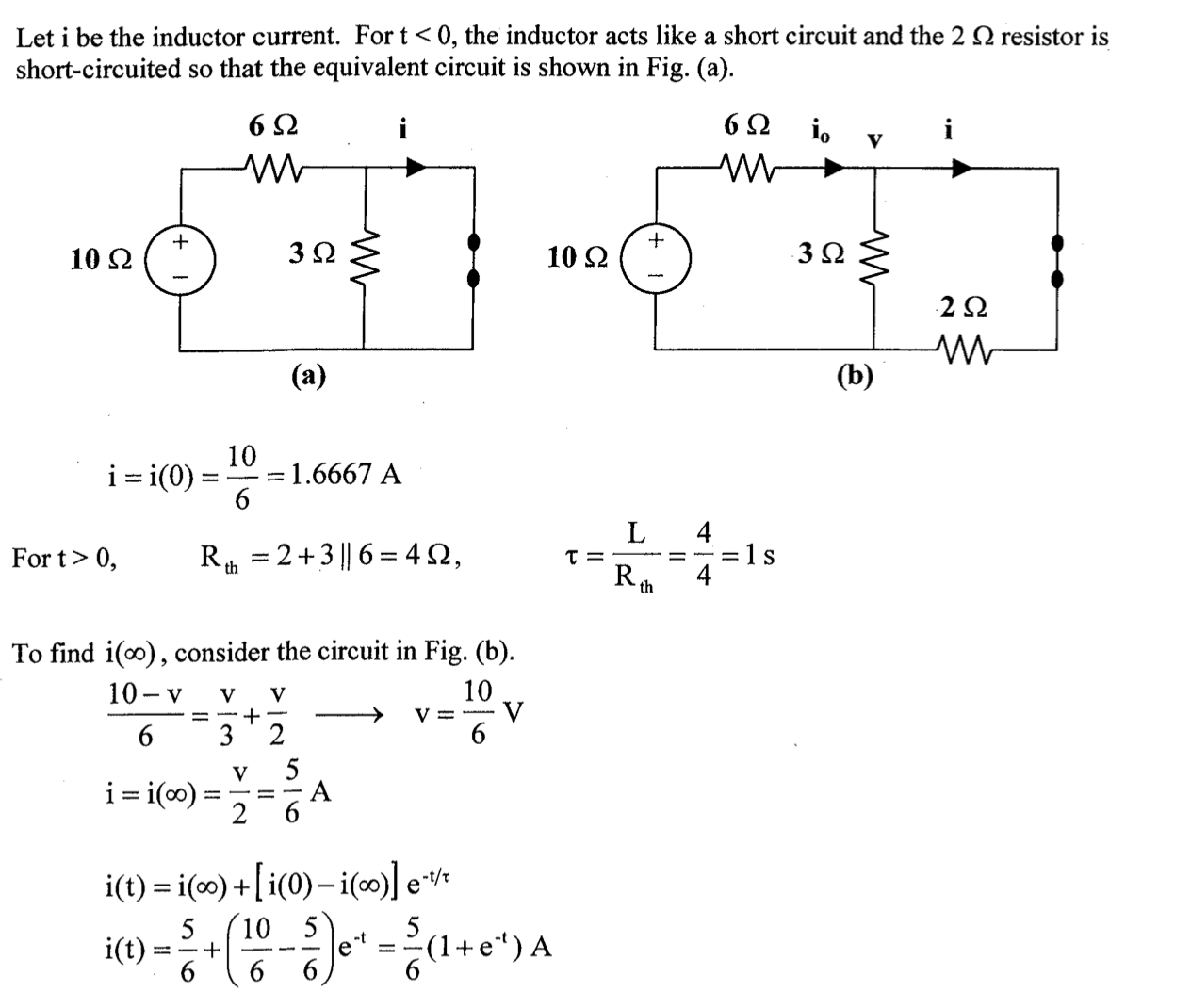
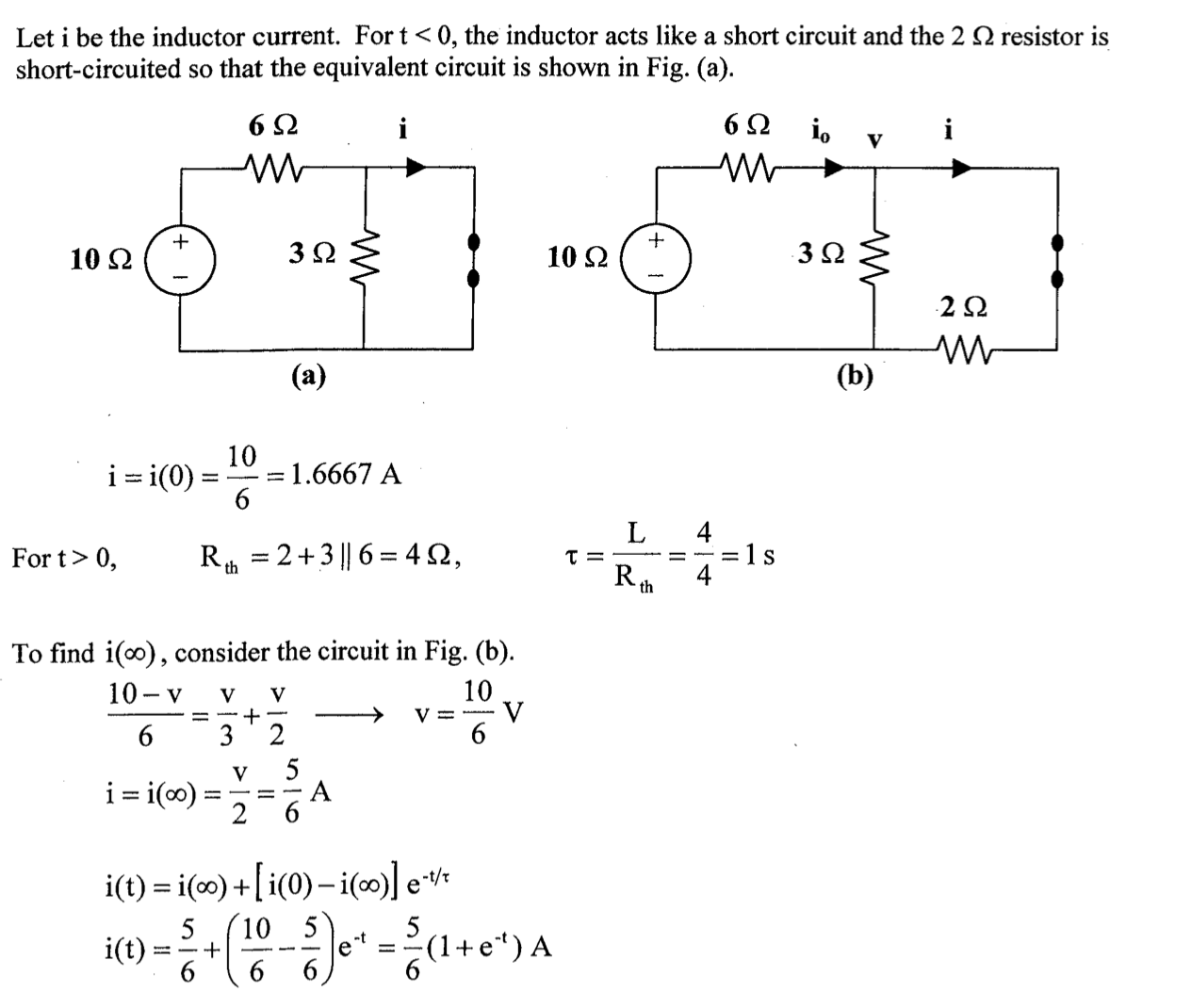
如图所示，若电感的初始电流 \(i(0)=12{\rm A}\)，求 \(t>0\) 时刻的 \(i(t)\) 和 \(v_x(t)\)

4-1-12.BtHLJ1Z8

初始条件 \(\Large i(0^+)=12{\rm A}\)

边界条件 \(\Large i(\infty)=0\)

对除了电感外的部分电路外施加电压 \(U\) 求等效电阻：

​ \(\Large \frac{U-v_x}{6}+\frac{U-v_x-2v_x}{2}=\frac{v_x}{1}\)

不妨取 \(\Large U=1{\rm V}\)，得：\(\Large v_x=0.25{\rm V}\)

​ \(\Large R_{eq}=\frac{U}{I}=\frac{1}{\frac{0.25}{1}}=4{\rm \Omega}\)

​ \(\Large \therefore \tau=\frac{L}{R_{eq}}=\frac{2}{4}=0.5{\rm s}\)

因此，\(\Large i(t)=i(\infty)+[i(0^+)-i(\infty)]e^{-\frac{t}{\tau}}=12e^{-2t}{\rm A}\)

​ \(\Large v_x(t)=-i \times 1=-12e^{-2t}{\rm A}\)

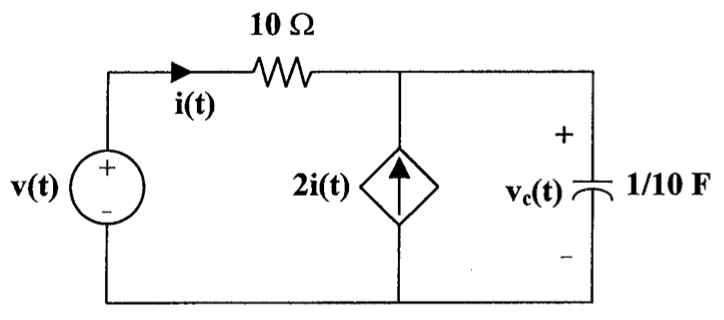
下图中，\(v(t) = 10[u(t)-u(t-2)]\) V，求 \(v_C(t)\)

1

image-20221016173645552.ebzM6Tm1

3

下图中，求 \(t>0\) 时刻的 \(v_o(t)\)

1

2

3